Graph theory in Computer competition

Intro

Graph theory is prabobly the most popular question in computer competition in USACO and NOIP(China). It is actually a branch of math theory. In the questions they would give you many points in a graph and ask you to find out the shortest way or the possile way to go from one point to another one. Sometimes it will provide you with values of the edge and ask you to calculate the smallest coast. Sounds pretty simple Hahhhhh. Let’s have a look!

Basic Information

PS: You can jump to next block and keep reading, and find the concept you don’t understand above.

Graph is a 2-tuple which describes the relationship between the points. Usually explained as G=(V,E), and V, E are mutiple sets.

Graph has two different types:

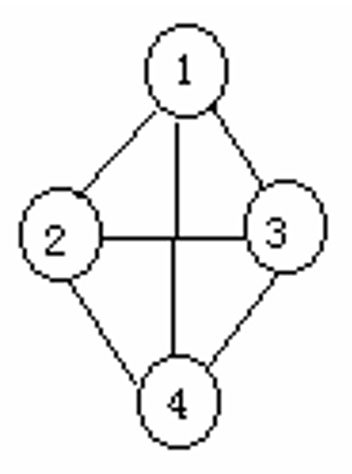
Undirected graph: Every elements in E are disordered 2-tuple(u,v), we name the element Undirected edge. And u,v$\in$V. Let e=(u,v), then u and v are e’s endpoint

Directed graph: Every elements in E are ordered 2-tuple, write as u$\longrightarrow$v, we name the element Directed edge. Let e=u$\longrightarrow$v, then u is e’s Tail, and v is e’s head.

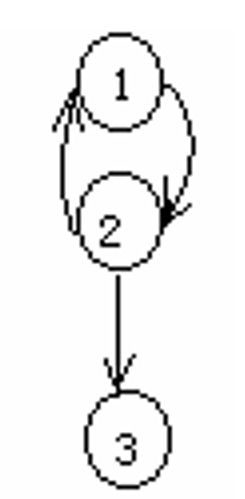
And for every elements in V, we call it Vertex or Node.

…….

Actually there is a lot more concept we need to know for the Graph Theory, but we are just programmers(~~I don’t want to write down~~) Here is the link for More basic info.

Restore the graph!

After we study the basic information, know we need to know how to restore those information about a graph in our computer.

There are three ways we use to restore graphs.

But to make it easy(~~I have no idea how to use the other two~~), I will only show the one that is most easy(~~Even can be mastered by the damn author~~)

Actually, Forward star can widely use on different kind of graphs, this is the main reason I introduce it.

Forward Star

We first use Struct to store the information about the graph.

We need to restore the basic info in the graph. Based on edge. So here are the info we need to restore in the struct: The value of the edge, the point the edge go to, the next edge.

So here is the code:

struct Edge{
       int dest;//destination
       int val;//edge's value
       int next;//next edge
  }eg[mx*2];//mx is the numer of the edges, if it is undirected you need to double
int n,m;//nomber of point in the graph，number of edge in the graph 
int head[MAX]={0};//The head in the graph
int top=0;//The exact number of the edeges

Then we add the data into the struct

void addedge(int u, int v, int val){ 
    eg[++top].dest=v;//v is the tail of the edge(destination)
    eg[top].val=val;//edge's value
    eg[top].next=head[u];//next edge's number
    head[u]=top;//Remeber this edge as another edge for the head u.
}

And here is the code in main function:

int main(){
int u,v,val,i;
   scanf(“%d%d”,&n,&m);
   for(i=1;i<=m;i++)//input the numer of edges
     scanf(“%d%d%d”,&u,&v,&val);//input the head, tail, and value
     addedge(u,v,val);//directed graph
     //addedge(v,u,val);//If it is undirected graph
   }
.....//Other code
}

This way we make the restorage logical and easy. Then we can actually do something with the theory.

Graph traversal

Find the relationship between two points in a graph can be seen as travel in the graph. And we need to know the basic how to travel through the whole graph.

void travel(int s){//Starting point
	for(i=head[s]; i ; i=eg[i].next){
       printf(“%d->%d=%d\n”,
       s,eg[i].dest,eg[i].val);
    }
}

But this kind of method is slow and do not fit most of the situation. We need some spcial methods.

Then here are two big basic alograithm for Graph theory.

DFS

DFS, full name Depth First Search.

To make it easy, the core of it is to follow one road till it is going to an end. We travel through every edges as long as the edge can be traveled through.

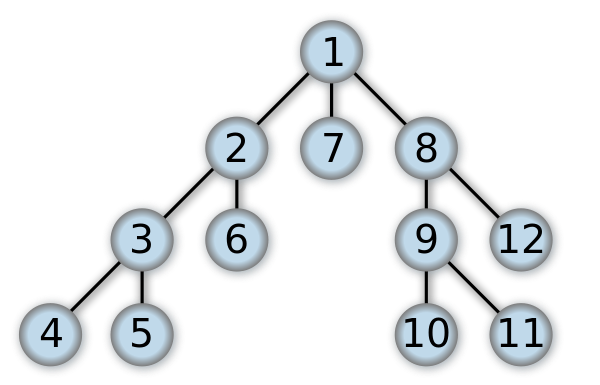
int vis[mx]={0};//To make sure you won't travel through the same edge over and over again
void dfs(int s){
	vis[s]=1;
	for(int i=head[s];i;i=eg[i].next){//travel
		if(!vis[eg[i].dest]){//haven't travel through
			dfs(eg[i].dest);//Then travel
		}
	}
}

Simple as this.

With the core of the dfs, we can solve some problems easily.

[USACO06DEC] Cow Picnic

Description

The cows are having a picnic! Each of Farmer John’s K (1 ≤ K ≤ 100) cows is grazing in one of N (1 ≤ N ≤ 1,000) pastures, conveniently numbered 1…N. The pastures are connected by M (1 ≤ M ≤ 10,000) one-way paths (no path connects a pasture to itself).

The cows want to gather in the same pasture for their picnic, but (because of the one-way paths) some cows may only be able to get to some pastures. Help the cows out by figuring out how many pastures are reachable by all cows, and hence are possible picnic locations.

Input

Line 1: Three space-separated integers, respectively: K, N, and M
Lines 2..K+1: Line i+1 contains a single integer (1..N) which is the number of the pasture in which cow i is grazing.
Lines K+2..M+K+1: Each line contains two space-separated integers, respectively A and B (both 1..N and A != B), representing a one-way path from pasture A to pasture B.

output

Line 1: The single integer that is the number of pastures that are reachable by all cows via the one-way paths.

Sample

Input

Output

Solution:

Dfs search every cows, use field[i] express the numer i field have been tracel through how many times, if field[i]=k then meet the standard(Means every cow has traveled through here).

#include <iostream>
#include<cstdio>
using namespace std;
const int mx=10005;//As the question given
struct edge{
	int dest,next;//No value given
}eg[mx];
int head[mx],top=0;
int vis[mx],field[1005],cow[105];
void addedge(int u,int v){
	eg[++top].dest=v,eg[top].next=head[u],head[u]=top;
}
void dfs(int s){
	vis[s]=1;field[s]++;
	for(int i=head[s];i;i=eg[i].next){
		if(!vis[eg[i].dest]){
			dfs(eg[i].dest);
		}
	}
}
int main() {
	int k,m,n,ans=0;
	std::ios::sync_with_stdio(false);//Speed up cin and cout
	cin>>k>>n>>m;
	for(int i=1;i<=k;i++){
		cin>>cow[i];
	}
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		addedge(u, v);//Directed graph
	}
	for(int i=1;i<=k;i++){
		for(int j=1;j<=n;j++){//Put vis back to 0 again
			vis[j]=0;
		}
		dfs(cow[i]);
	}
	for(int i=1;i<=n;i++){
		if(field[i]==k)ans++;
	}
	cout<<ans;
	return 0;
}

BFS

BFS, full name Breadth First Search

BFS is a traversing algorithm where you should start traversing from a selected node (source or starting node) and traverse the graph layerwise thus exploring the neighbour nodes (nodes which are directly connected to source node). You must then move towards the next-level neighbour nodes.

Code:

#include<queue>//Import queue libaray
queue<int>q;//Declare queue
void bfs(int s){
	q.push(s);vis[s]=1;//push s into the queue and vis
	while(!q.empty()){//As long as there is still elements in the queue
		int u=q.front();//Get the front of the queue
		q.pop();//Get the front of the queue out
		for(int i=head[u];i;i=eg[i].next){//Same old story
			int v=eg[i].dest;
			if(!vis[v]){
				q.push(v),vis[v]=1;
			}
		}
	}
}

Example

[USACO14DEC] Piggy Back

Description

Bessie and her sister Elsie graze in different fields during the day, and in the evening they both want to walk back to the barn to rest. Being clever bovines, they come up with a plan to minimize the total amount of energy they both spend while walking.

Bessie spends B units of energy when walking from a field to an adjacent field, and Elsie spends E units of energy when she walks to an adjacent field. However, if Bessie and Elsie are together in the same field, Bessie can carry Elsie on her shoulders and both can move to an adjacent field while spending only P units of energy (where P might be considerably less than B+E, the amount Bessie and Elsie would have spent individually walking to the adjacent field). If P is very small, the most energy-efficient solution may involve Bessie and Elsie traveling to a common meeting field, then traveling together piggyback for the rest of the journey to the barn. Of course, if P is large, it may still make the most sense for Bessie and Elsie to travel

separately. On a side note, Bessie and Elsie are both unhappy with the term “piggyback”, as they don’t see why the pigs on the farm should deserve all the credit for this remarkable form of

transportation.

Given B, E, and P, as well as the layout of the farm, please compute the minimum amount of energy required for Bessie and Elsie to reach the barn.

Input

INPUT: (file piggyback.in)

The first line of input contains the positive integers B, E, P, N, and M. All of these are at most 40,000. B, E, and P are described above. N is the number of fields in the farm (numbered 1..N, where N >= 3), and M is the number of connections between fields. Bessie and Elsie start in fields 1 and 2, respectively. The barn resides in field N.

The next M lines in the input each describe a connection between a pair of different fields, specified by the integer indices of the two fields. Connections are bi-directional. It is always possible to travel from field 1 to field N, and field 2 to field N, along a series of such connections.

output

OUTPUT: (file piggyback.out)

A single integer specifying the minimum amount of energy Bessie and

Elsie collectively need to spend to reach the barn. In the example

shown here, Bessie travels from 1 to 4 and Elsie travels from 2 to 3

to 4. Then, they travel together from 4 to 7 to 8.

Sample

Input:

Output

Solution:

Because the shortest distance from one point to the destination is unchangable, so we don’t have to consider two of them meet together and depart. If B+E*<=P , then we should keep them being together；
If B+E >*P Then they’d better be apart.
So we only need to run bfs from 1,2,n. And get the shortest length. After we enumerate the points they will be together, we are done.

#include <iostream>
#include<cstdio>
#include<queue>
using namespace std;
const int mx=40005;
struct edge{
	int dest,next;
}eg[mx];
int head[mx],top=0,vis[3][mx],dis[3][mx];//dis[][]is used to memorize the distance
int b,e,p,n,m,u,v;
void addedge(int u,int v){//Same old story
	eg[++top].dest=v;
	eg[top].next=head[u];
	head[u]=top;
}
queue<int>q;
void bfs(int s){
	if(s==0) vis[s][1]=1,q.push(1);//
	else if(s==1) vis[s][2]=1,q.push(2);
	else vis[s][n]=1,q.push(n);
	while(!q.empty()){
		int u=q.front();q.pop();
		for(int i=head[u];i;i=eg[i].next){
			int v=eg[i].dest;
			if(!vis[s][v]){
				dis[s][v]=dis[s][u]+1;//The distance to the head=the distance to the tail + 1
				q.push(v);
				vis[s][v]=1;	
			}
		}
	}
}
int main() {
	std::ios::sync_with_stdio(false);
	cin>>b>>e>>p>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>u>>v;
		addedge(u,v);
		addedge(v, u);//undirected graph
	}
	bfs(0);
	bfs(1);
	bfs(2);
	int ans=1e9;//Put ans to largest int, or it will be hard to replace with new value
	for(int i=1;i<=n;++i){
		ans=min(ans, dis[0][i]*b+dis[1][i]*e+dis[2][i]*p);//As the question said
	}
	cout<<ans;
	return 0;
}

More advanced Algotithm

Dijkstra

It uses the idea of BFS, aims to solve the Shortest path problem. It works both well for Directed graph and undirected graph.

The point of Djikstra is be greedy. We declare an array to restore the distance from the starting point to another point, initialize them as infinite number if there is no direct edge from starting point to them, and if they do have, put them as the smae value as the value of the edge .So that we can replace them with smaller number which we gained from the value of the route. As the graph.

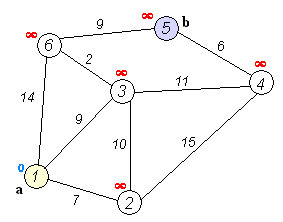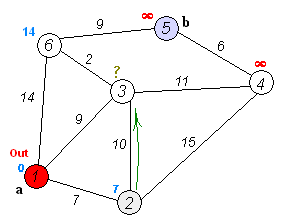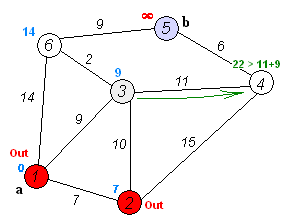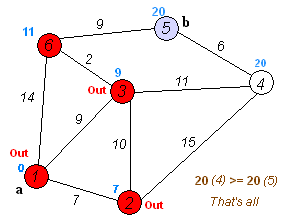
Dijkstra has Time complexity 𝑂(n^2), but with heap, it can be 𝑂((𝑛+𝑚)log2𝑛)

struct node{//Declare another struct to restore the information for the point
	int dis,pos;//pos means the number of the point
	bool operator <( const node &x )const{//declare the operator '<' by our own function
		return x.dis < dis;
	}
};
std::priority_queue<node> q;//priority queue
int dis[mx],vis[mx];
void dijkstra(int s){
	dis[s]=0;
	q.push((node){0,s});//push into queue as struct node
	while(!q.empty()){
		node tmp=q.top();q.pop();
		int x=tmp.pos,d=tmp.dis;
		if(!vis[x]){//Got to the tail, if we didn't visit it
		vis[x]=1;
		for(int i=head[x];i;i=eg[i].next){
			int y=eg[i].dest;
			if(dis[y]>dis[x]+eg[i].val){
				dis[y]=dis[x]+eg[i].val;//The core of the code, to replace for smaller
				if(!vis[y])//Got to the head, if we didn't visit it
					q.push((node){dis[y],y});
				}
			}
		}
	}
}

[USACO19DEC]Milk Pumping G

Description

Farmer John has recently purchased a new farm to expand his milk production empire. The new farm is connected to a nearby town by a network of pipes, and FJ wants to figure out the best set of these pipes to purchase for his use in pumping milk from the farm to the town.

The network of pipes is described by NN junction points (endpoints of pipes), conveniently numbered 1…N1…N (2≤N≤10002≤N≤1000). Junction point 1 represents FJ’s farm and junction point NN is the town. There are MM bi-directional pipes (1≤M≤10001≤M≤1000), each joining a pair of junction points. The iith pipe costs cici dollars for FJ to purchase for his use, and can support a flow rate of fifi liters of milk per second.

FJ wants to purchase a single path worth of pipes, where the endpoints of the path are junctions 1 and NN. The cost of the path is the sum of the costs of the pipes along the path. The flow rate along the path is the minimum of the flow rates of the pipes along the path (since this serves as a bottleneck for the flow traveling down the path). FJ wants to maximize the flow rate of the path divided by the cost of the path. It is guaranteed that a path from 11 to NN exists.

Input

The first line of input contains NN and M.M. Each of the following MM lines describes a pipe in terms of four integers: aa and bb (the two different junctions connected by the pipe), cc (its cost), and ff (its flow rate). Cost and flow rate are both positive integers in the range 1…10001…1000.

output

Please print 106106 times the optimal solution value, truncated to an integer (that is, rounded down to the next-lowest integer if this number is not itself an integer).

Sample

Input:

1
2
3

3 2
2 1 2 4
2 3 5 3

Output

Solution:

Just enumerate the biggest flow from 1 to 1000, and calculate for the smallest cost.

#include <iostream>
#include<queue>
#include<cstdio>
using namespace std;
const int mx=2010;
const int INF=1e9+7;
struct edge{
	int dest,val,next,flow;
}eg[mx*2];
int head[mx],top=0,vis[mx],dis[mx];
int n,m,ans=0;
void addedge(int u,int v,int val,int flow){//Same old story
	eg[++top].dest=v;
	eg[top].val=val;
	eg[top].flow=flow;
	eg[top].next=head[u];
	head[u]=top;
}
queue<int>q;
void dij(int flow){
	  for(int i=1;i<=n;i++)dis[i]=INF,vis[i]=0;//Initialize dis and vis
			dis[1]=0,vis[1]=1;
			q.push(1);
			while(!q.empty()){
				int u=q.front();q.pop();vis[u]=0;
				for(int i=head[u];i;i=eg[i].next){
					if(eg[i].flow<flow)continue;//Means we have already enumerated
					int t=eg[i].dest;
					if(dis[u]+eg[i].val<dis[t]){//Everything can change, the core never change
						dis[t]=dis[u]+eg[i].val;
						if(!vis[t]){
							vis[t]=1;
							q.push(t);
						}
					}
				}
			}
			if(dis[n]!=INF)ans=max(ans,flow*1000000/dis[n]);//We got to the end, see if we can replace
}
int main() {
	std::ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		addedge(a, b, c, d);
		addedge(b, a, c, d);
	}
	for(int i=1;i<=1000;i++)//from 1 to 1000 enumerate the smallest flow
	dij(i);
	cout<<ans;
	return 0;
}

Floyd

It solve the Shortest path problem between two points, unlike Dijkstra, Floyd allow us to deal with the edge which has negative value. But Floyd take more time complexity(O(n^3)). So we have to be careful about it.

Like Dijkstra, Floyd’s core is also enumerate. It enumerate every point by 3 for loops. Because we suppose there is a shorter way than directly get to the point. We use g[i] [j] to express the distance from i to j, so there might be a point k in between might make this case:

1	g[i][j]>g[i][k]+g[k][j];

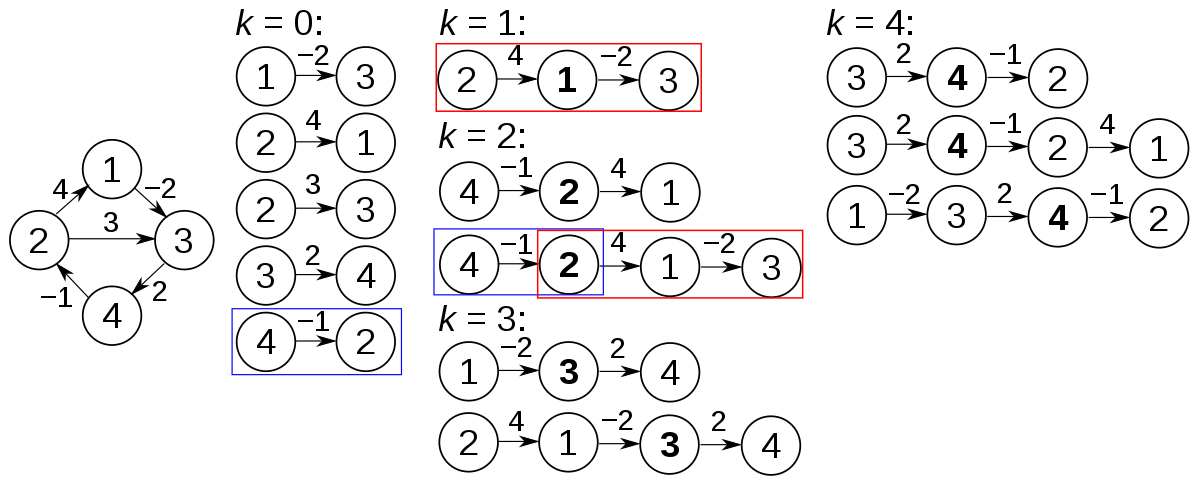
I think it is easier to understand by code:(Probably the shortest one you ever meet)

void floyd(){
	for(int k=1;k<=n;k++) {
		for(int i=1; i<=n; i++) {
			for(int j=1; j<=n; j++) {
				if(g[i][k]<inf&&g[k][j]<inf&&g[i][j]>g[i][k]+g[k][j])
					g[i][j]=g[i][k]+g[k][j];
			}
		}
	}
}

[USACO09DEC]Cow Toll Paths

Description

Like everyone else, FJ is always thinking up ways to increase his revenue. To this end, he has set up a series of tolls that the cows will pay when they traverse the cowpaths throughout the farm.

The cows move from any of the N (1 <= N <= 250) pastures conveniently numbered 1..N to any other pasture over a set of M (1 <= M <= 10,000) bidirectional cowpaths that connect pairs of different pastures A_j and B_j (1 <= A_j <= N; 1 <= B_j <= N). FJ has assigned a toll L_j (1 <= L_j <= 100,000) to the path connecting pastures A_j and B_j.

While there may be multiple cowpaths connecting the same pair of pastures, a cowpath will never connect a pasture to itself. Best of all, a cow can always move from any one pasture to any other pasture by following some sequence of cowpaths.

In an act that can only be described as greedy, FJ has also assigned a toll C_i (1 <= C_i <= 100,000) to every pasture. The cost of moving from one pasture to some different pasture is the sum of the tolls for each of the cowpaths that were traversed plus a single additional toll that is the maximum of all the pasture tolls encountered along the way, including the initial and destination pastures.

The patient cows wish to investigate their options. They want you to write a program that accepts K (1 <= K <= 10,000) queries and outputs the minimum cost of trip specified by each query. Query i is a pair of numbers s_i and t_i (1 <= s_i <= N; 1 <= t_i <= N; s_i != t_i) specifying a starting and ending pasture.

Consider this example diagram with five pastures:

The ‘edge toll’ for the path from pasture 1 to pasture 2 is 3. Pasture 2’s ‘node toll’ is 5.

To travel from pasture 1 to pasture 4, traverse pastures 1 to 3 to 5 to 4. This incurs an edge toll of 2+1+1=4 and a node toll of 4 (since pasture 5’s toll is greatest), for a total cost of 4+4=8.

The best way to travel from pasture 2 to pasture 3 is to traverse pastures 2 to 5 to 3. This incurs an edge toll of 3+1=4 and a node toll of 5, for a total cost of 4+5=9.

Input

* Line 1: Three space separated integers: N, M, and K

* Lines 2..N+1: Line i+1 contains a single integer: C_i

* Lines N+2..N+M+1: Line j+N+1 contains three space separated

integers: A_j, B_j, and L_j

* Lines N+M+2..N+M+K+1: Line i+N+M+1 specifies query i using two space-separated integers: s_i and t_i

output

* Lines 1..K: Line i contains a single integer which is the lowest cost of any route from s_i to t_i

Sample

Input:

Output

1
2

8 
9

Solution:

N so small and asking so many. Definally Floyd. We use two arries dis[][] and dist[][] to memorize the value of the edges alone and the value of the edges add with the value of points. We enumerate the value of points from small to big for point k, then the last k we enumerate should have the biggest point value from a to b. And we compare it with i and j’s value we then get the biggest point value. Then we are done.

#include <iostream>
#include<cstdio>
#include<cstring>//memset
#include<algorithm>//For sort
using namespace std;
int n,m,k,dis[300][300],dist[300][300],c[300];//dis without point value, dist is with
struct node{
	int d,id;
}x[300];
bool cmp(node a,node b){//use in the sort function
	if(a.d==b.d)
		return a.id<b.id;
	return a.d<b.d;
}
void floyd(){//Same old story
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++){
				if(i==j) continue;
				dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//Our original Floyd
				dist[i][j]=min(dist[i][j],dis[i][j]+max(x[k].d,max(x[i].d,x[j].d)));//As said in the question
			}
}
int main(){
	std::ios::sync_with_stdio(false);
	cin>>n>>m>>k;
	memset(dis,0x3f,sizeof(dis));
	for(int i=1;i<=n;i++){
		cin>>x[i].d;
		x[i].id=i;
		dis[i][i]=0;
	}
	sort(x+1,x+1+n,cmp);//sort by the value of point
	int origin[300];
	for(int i=1;i<=n;i++)origin[x[i].id]=i;//question will ask the origin number, let's memorize it
	for(int i=1;i<=m;i++){
		int a,b,c;
		cin>>a>>b>>c;
		dis[origin[a]][origin[b]]=dis[origin[b]][origin[a]]=min(dis[origin[b]][origin[a]],c);
	}
	memset(dist,0x3f,sizeof(dist));
	floyd();
	for(int i=1;i<=k;i++){
	int a,b;
	cin>>a>>b;
	cout<<(dist[origin[a]][origin[b]])<<endl;
	}
	return 0;
}

SPFA

SPFA, full name Shortest Path Faster Algorithm.

Sounds pretty cool Hahhh. Actually, I think it is the most useful algorithm for graph theory, it can deal with almost all kinds of graph. Now, let’s see how it works!

It works by repeatedly selecting a vertex and using it to relax, if possible, all of its neighbors. If a node was successfully relaxed, then it might in turn be necessary to use it to relax other vertices, and hence it is marked for consideration also. Once there are no vertices left to be considered, the algorithm terminates. Note that a vertex might be considered several times during the course of the algorithm. The usual implementation strategy is to use a queue to hold the vertices that might be considered next.

Code:

void spfa(int s){
	int u,v;    memset(dist,0x3f,sizeof(dist));//Initialize dist
	dist[s]=0;//Get start point as 0
	inque[s]=1;//Memorize the s is in the queue
	q.push(s);//in queue
	while(!q.empty()){
		u=q.front(), q.pop();  inque[u]=0;//Get the front of queue out
		for(int i=head[u]; i; i=eg[i].next){
			  v=eg[i].dest;
			  if(dist[v]>dist[u]+eg[i].val){//If find a route with smaller value
				  dist[v]= dist[u]+eg[i].val;//change it 
				  fa[v]=u;//Memorize the tail of v
				  if(!inque[v]){
					  q.push(v), inque[v]=1;
				  }
			  }
		}
	}
}

We see that spfa is pretty similar to Dijkstra. let me use the core code to express the difference.

Difference between Dij+heap and SPFA!!!

Dij:

while(!q.empty()){
  //If priority queue is not empty
		node tmp=q.top();q.pop();
  //get top out
		int x=tmp.pos,d=tmp.dis;
		if(!vis[x]){//Got to the tail, if we didn't visit it
		vis[x]=1;
		for(int i=head[x];i;i=eg[i].next){
			int y=eg[i].dest;
			if(dis[y]>dis[x]+eg[i].val){
        //Relax
				dis[y]=dis[x]+eg[i].val;//The core of the code, to replace for smaller
				if(!vis[y])//Got to the head, if we didn't visit it
					q.push((node){dis[y],y});
        //New distance and new point into the queue
				}
			}
		}
	}

SPFA:

while(!q.empty()){
   //if regular queue is not empty
	u=q.front(), q.pop();  inque[u]=0;//Get the front of queue out
   //Get top out
   //And Remember!!!
	for(int i=head[u]; i; i=eg[i].next){
		  v=eg[i].dest;
		  if(dist[v]>dist[u]+eg[i].val){//If find a route with smaller value
         //Relax
			  dist[v]= dist[u]+eg[i].val;//change it 
			  fa[v]=u;//Memorize the tail of v
			  if(!inque[v]){
           //the points that are Relaxed but not in queue get into the queue
				  q.push(v), inque[v]=1;
			  }
		  }
	}
}

So the difference is clear enough:

Dji+heap: Small root pile, every time get the shortest distance, for this point, the shortest distance won’t change!

SPFA: Use queue. Get the front out of queue, might be renew in the future, it is won’t be always the same.

[USACO14OPEN]Dueling GPS’s

Description

Farmer John has recently purchased a new car online, but in his haste he accidentally clicked the “Submit” button twice when selecting extra features for the car, and as a result the car ended up equipped with two GPS navigation systems! Even worse, the two systems often make conflicting decisions about the route that FJ should take.

The map of the region in which FJ lives consists of N intersections (2 <= N <= 10,000) and M directional roads (1 <= M <= 50,000). Road i connects intersections A_i (1 <= A_i <= N) and B_i (1 <= B_i <= N). Multiple roads could connect the same pair of intersections, and a bi-directional road (one permitting two-way travel) is represented by two separate directional roads in opposite orientations. FJ’s house is located at intersection 1, and his farm is located at intersection N. It is possible to reach the farm from his house by traveling along a series of directional roads.

Both GPS units are using the same underlying map as described above; however, they have different notions for the travel time along each road. Road i takes P_i units of time to traverse according to the first GPS unit, and Q_i units of time to traverse according to the second unit (each travel time is an integer in the range 1..100,000).

FJ wants to travel from his house to the farm. However, each GPS unit complains loudly any time FJ follows a road (say, from intersection X to intersection Y) that the GPS unit believes not to be part of a shortest route from X to the farm (it is even possible that both GPS units can complain, if FJ takes a road that neither unit likes).

Please help FJ determine the minimum possible number of total complaints he can receive if he chooses his route appropriately. If both GPS units complain when FJ follows a road, this counts as +2 towards the total.

Input

* Line 1: The integers N and M.

Line i describes road i with four integers: A_i B_i P_i Q_i.

output

* Line 1: The minimum total number of complaints FJ can receive if he routes himself from his house to the farm optimally.

Sample

Input:

Output

Solution:

At first we need to know the shortest path for both GPS. And we need to know every point’s distance from the end point n, there is no way we need to use other alogrithm, we can just run sofa from n. How can we calculate how many time the GPS complained? We can simplely enumerate every edge, to see if its value is equal to the head and tail’s shortest length, and use dist[] to memorize how many time will the GPS complain if we across this route. Then we creat a new map based on this dist[], and spfa find the smallest path.

#include <iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int mx=100005;
const int INF=0x3f3f3f;
struct Edge{//Same old story
	int next,dest,val;
}eg[4][mx];
int n,m,head[4][mx],top=0,a,b,p,h;//We need three maps
int dist[100005];bool vis[100005];
void addedge(int u,int v,int val,int mode){//Same old story just have double the array
	eg[mode][top].next=head[mode][u];eg[mode][top].dest=v;
	eg[mode][top].val=val;head[mode][u]=top;
}
queue<int>q;
void spfa(int s,int mode){
		queue<int>q;
		memset(dist,0x7f,sizeof(dist));
		memset(vis,0,sizeof(vis));
		q.push(s);
		vis[s]=true;
		dist[s]=0;
		while(!q.empty()){
			int u=q.front();
			q.pop();
			for(int i=head[mode][u];i;i=eg[mode][i].next){
				if(dist[eg[mode][i].dest]>dist[u]+eg[mode][i].val){
					dist[eg[mode][i].dest]=dist[u]+eg[mode][i].val;
					if (!vis[eg[mode][i].dest]){
						q.push(eg[mode][i].dest);
						vis[eg[mode][i].dest]=1;
					}
				}
			}
			vis[u]=0;
		}
		//The important part of this question
		if(mode==3) cout<<dist[n];
		else{
			for(int i=1;i<=n;i++){//enumerate every points
				for(int j=head[mode][i];j;j=eg[mode][j].next){
					if (dist[i]+eg[mode][j].val==dist[eg[mode][j].dest]){
						eg[3][j].val--;//For edges in the shortest path, renew it
					}
				}
			}
		}
}
int main(){
	std::ios::sync_with_stdio(false);
	memset(head,-1,sizeof(head));
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		top++;
		cin>>a>>b>>p>>h;
		addedge(b,a,p,1);
		addedge(b,a,h,2);
		addedge(a,b,2,3);
	}
	spfa(n,1);
	spfa(n,2);
	spfa(1,3);
	return 0;
}

Conclusion

In this blog we studied DFS, BFS, Dijkstra, Floyd, and SPFA. They have their own advantages so we need to use them properly in competition. Here are a chart about each. Hopefully this woould be helpful to you.