Data Structure: Tree

Intro

In computer science, a data structure is a data organization, management, and storage format that enables efficient access and modification. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data

Basic Info

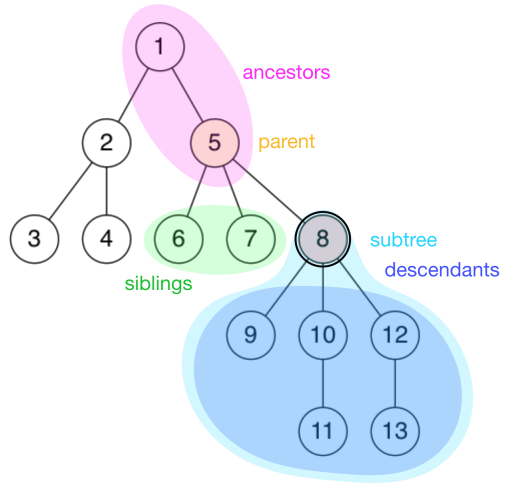
Tree in computer science is the same as the tree in the real world. But we are more used to put the root on the top to think about the tree.

A tree without any stable point is unrooted tree, it has those equalievent definition:

• Has n points, n-1 edges linked undirected graph
• Undirected graph but without cycle
• Undirected graph which two points have and only have a simple path

In the base as the unrooted graph, the specific point is root.

Restore it!

Segment tree

In computer science, a segment tree, also known as a statistic tree, is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, it’s a structure that cannot be modified once it’s built. A similar data structure is the interval tree. A segment tree for a set I of n intervals uses O(n log n) storage and can be built in O(n log n) time. Segment trees support searching for all the intervals that contain a query point in O(log n + k), kbeing the number of retrieved intervals or segments.

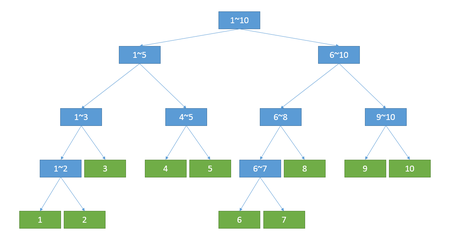
So it has every characteristic binary tree has:

• There are at most 2^(i-1)^(i$>=$1) points in the number i layer of the binary tree

• There are at most 2^(i-1)^(i$>=$1) points in the binary tree which’s depth is i

• A binary tree which has n points has log2^n^+1 depth

• For a perfect binary tree which has n points, for any point i(1<=i<=n):

  If i==1, then i is the root of the binary tree, else if i>1, then i’s parent is i/2

  if 2i>n, then i has no left child

  If 2i+1>n, then i has no right child

Charastics of Segment tree

• almost perfect binary tree.

• i’s father is i/2(suppose i is a point in the tree)

• i’s brothers are b=i/2*2andanother one is b+1.

• i’s children are l=i*2and r=l+1

Restoring

Base on the charastic of the binary tree. We can easily build the Segment tree.

Because the segment tree, every point has larger value which is stored in one of its children. So we need to store its children in order to know the segment. And also the value of the point of course. Because the question would ask the data in the original order, so we also need to store those info.

const int mx=100001; 
typedef long long ll; 
struct Node { 
    int l, r; //left son and right son
    ll val; //The largest value
}  tr[mx<<2] ;//mx<<2 is equal to mx*2.
int n, a[mx]= {0};//points number, the array restoring data
int real[mx]={0};//The real poisition for the leaves

Building

We build the tree from its root, then its sons. Then we keep build sons’s sons through recursion. And when we finally get to the deepest point of the tree(leaves). We need to memerozie the number for the leaves and restore the value.

void build(int i, int l, int r){
   tr[i].l=l, tr[i].r=r, tr[i].val=0;
   if(l==r){ //if reach the leaf point
     real[l]=i; //memerozie the number for the leaves
     tr[i].val=a[l]; // restore the value
     return;//End the function
   }
   int m=(l+r)>>1; //Midpoint
   build(i<<1,l,m); //Left son
   build(i<<1|1,m+1,r); //right son
   tr[i].val=max(tr[i<<1].val,tr[i<<1|1].val);//Renew the value of the father ponint through son's point
}

Query segment

Query will return the max value for the segment. So it will firtst find out if the request segment is in the domain, and return the value.

long long query(int i,int l,int r){
	if(tr[i].l>=l&&tr[i].r<=r)return tr[i].val;//In range
	if(tr[i].l>r||tr[i].r<l)return 0;//not in
	return max(tr[i<<1].val, tr[i<<1|1].val);//Else return the max in sons
}

Update value（One point）

Once we changed a point. It will influence its father and all the way to the root.

 tr[real[a]].val=k;//IN the main func, change the value of a point
void update(int i){
   if(i==1) return;//To the root
   int fi=i>>1;//calculate its father
   tr[fi].val=max(tr[fi<<1].val, tr[fi<<1|1].val);
   update(fi);//Update father
}

Update Value(Segment)

When we trying to update the value for a segment, it is impossible to update one point by one pointO(nlogn). So we add a lazy tag which store the value that need to be updated. So the segment update will be more like query segment. So we need to discuss If the segment we need to update is inside the segment…….

void build(int i,int l,int r) { 
tr[i].l=l,tr[i].r=r,tr[i].val=0,tr[i].lazy=0; 
if(l==r) {  tr[i].val=a[l];  return;}
int mid=(l+r)>>1; //Same old story
build(i<<1,l,mid); 
build(i<<1|1,mid+1,r);
tr[i].val=tr[i<<1].val+tr[i<<1|1].val; //It can also restore the value of the sum
} 
void update(int i,int l,int r,int k) { //K is the value we need to update
  if(l<=tr[i].l&&r>=tr[i].r) {//If just inside the segment i
    tr[i].lazy+=k; //add k to lazy value
    tr[i].val+=(tr[i].r-tr[i].l+1)*k; //add k to the segment
    return;
  } 
  if(r<tr[i].l||l>tr[i].r)return; // If it is not inside the segment i
  
  pushdown(i);//Pushdown the value from the father segment
  
  update(i<<1,l,r,k); //Same old story
  update(i<<1|1,l,r,k); 
  tr[i].val=tr[i<<1].val+tr[i<<1|1].val;//In this kind, the value can only restore the summary of its son's value
} 
void pushdown(int i) { 
if(tr[i].lazy==0) return;//Don't need to update
tr[i<<1].lazy+=tr[i].lazy;//pass lazy to left son
tr[i<<1].val+=tr[i].lazy*(tr[i<<1].r-tr[i<<1].l+1); //Update value of left son
tr[i<<1|1].lazy+=tr[i].lazy;//right son
 tr[i<<1|1].val+=tr[i].lazy*(tr[i<<1|1].r-tr[i<<1|1].l+1);
 	tr[i].lazy=0;//The value has passed
 } 
long long query(int i,int l,int r){
	if(tr[i].l>=l&&tr[i].r<=r)return tr[i].val;//In range
	if(tr[i].l>=r||tr[i].r<=l)return 0;//not in
  pushdown(i); //Update the value from the father point
	return query(i<<1,l,r)+query(i<<1|1,l,r);
}

Now we know the way to update the value for a segment.

How about the segment’s value time something?（Discussion question）

Binary Indexed Tree

A data structure that can efficiently update elements and calculate prefix sums in a table of numbers.

We can understand it through segment tree. The Binary indexed tree aims to calculate the sum from a_s

a_s+1…..a_t. We can calculate it with segment tree. But what if we want to get it fast? If we can calculate the sum(1t)-the sum(1s-1), it works the same. Then we discover that the right son is no longer needed. We can get them from the father - left son.


So base on the graph below.


Everytime we minus the last 1 in the binary expression, and add i’s value into the result, we can get the sum easily. This is the importance of lowbit.

i	Binary Expression
5	0101
4	0100
0	0000

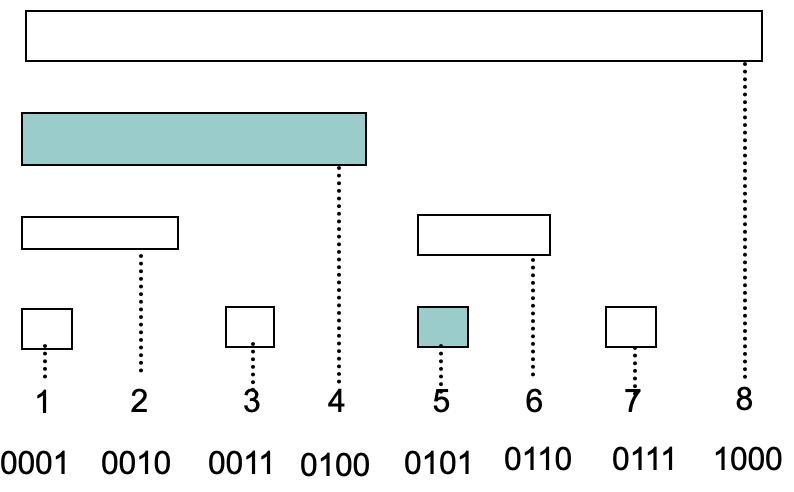
When we update the data, we just add 0001 to the binary expression.

i	Binary Expression
5	0101
6	0110
8	1000

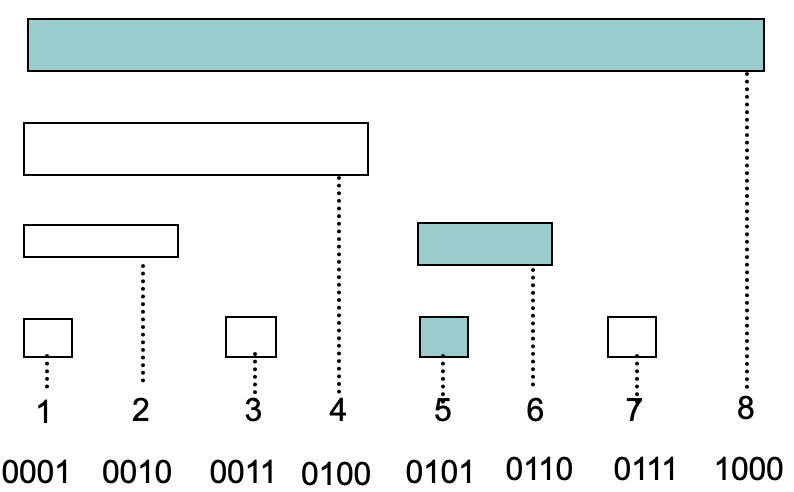
Preparation: lowbit()

Lowbit(i) will return the place for 1 in the binary system.

For instance, lowbit(10)will return 2 because (10)₂=1010. And 1 is in the place 2.

int lowbit(int x){
   return x & -x;
}

Realization

int bit[mx+1], n;
int lowbit(int x){
   return x & -x;
}
int sum(int i){//Calculate the sum
  int s =0;
  while(i>0){
    s+=bit[i];  i-=lowbit(i);
  }
}
void add(int i, int x){//Add x to i
    while(i<=n){
       bit[i]+=x; i+=lowbit(i);
   }
}

Binary Indexed tree & Inversion

Inversion

For a sequence A. If i<j and A[i]>A[j]. We call A[i] and A[j] are inversion.

So we can find the number of the inversion in this way

int cnt = 0;
for (int i = A.size() - 1; i >= 0; --i) {
    cnt += sum(A[i]);
    update(A[i], 1);
}

Example

Description

Every year, Farmer John’s N (1 <= N <= 20,000) cows attend “MooFest”,a social gathering of cows from around the world. MooFest involves a variety of events including haybale stacking, fence jumping, pin the tail on the farmer, and of course, mooing. When the cows all stand in line for a particular event, they moo so loudly that the roar is practically deafening. After participating in this event year after year, some of the cows have in fact lost a bit of their hearing.

Each cow i has an associated “hearing” threshold v(i) (in the range 1..20,000). If a cow moos to cow i, she must use a volume of at least v(i) times the distance between the two cows in order to be heard by cow i. If two cows i and j wish to converse, they must speak at a volume level equal to the distance between them times max(v(i),v(j)).

Suppose each of the N cows is standing in a straight line (each cow at some unique x coordinate in the range 1..20,000), and every pair of cows is carrying on a conversation using the smallest possible volume.

Compute the sum of all the volumes produced by all N(N-1)/2 pairs of mooing cows.

Input

* Line 1: A single integer, N

* Lines 2..N+1: Two integers: the volume threshold and x coordinate for a cow. Line 2 represents the first cow; line 3 represents the second cow; and so on. No two cows will stand at the same location.

Output

* Line 1: A single line with a single integer that is the sum of all the volumes of the conversing cows.

Sample Input

4
3 1
2 5
2 6
4 3

Sample Output

57

Solution

Of course stimulation can be a good way, easy to think. But use the binary indexed tree can help to save a lot of time. So we sort cows first because when data is sorted from the smallest to the largest, we don’t need to worry about computation. So we need to use struct to restore the value. But we can’t make sure the x value for a cow, we must come up with a way to calculate the cows ( who are before cow i and x<x_i)’s sum of x’s absolute value.

So we need to use two Binary Indexed tree to restore the data:

• The number of cows which are before i and x are smaller than x_i
• The cows which are before i and x are smaller than x_i, the sum of their x value

#include <iostream>
using namespace std;
typedef  long long ll;
const int mx=50010;
ll n,bit[mx],bit2[mx];
struct Cow{
	ll v,d;
}c[mx];
bool cmp(Cow a,Cow b){
	return a.v<b.v;
}
//Binary index tree 1
ll lowbit(ll x){
	return x&(-x);
}
void add(int x,int k){
	while(x<mx){
		bit[x]+=k;
		x+=lowbit(x);
	}
}
ll sum(int i){
	ll s=0;
	while(i>0){
		s+=bit[i];
		i-=lowbit(i);
	}
	return s;
}
//Binary index tree 1
void add2(int x,int k){
	while(x<mx){
		bit2[x]+=k;
		x+=lowbit(x);
	}
}
ll sum2(int i){
	ll s=0;
	while(i>0){
		s+=bit2[i];
		i-=lowbit(i);
	}
	return s;
}
int main() {
	std::ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>c[i].v>>c[i].d;
	sort(c+1,c+1+n,cmp);//The cmp is write especially for structure
	ll ans=0,all=0;
	for(int i=1;i<=n;i++){
		ll s1=sum(c[i].d),s2=sum2(c[i].d);
		ans+=(s1*c[i].d-s2)*c[i].v;
		ans+=((all-s2)-(i-1-s1)*c[i].d)*c[i].v;
			add(c[i].d,1);
			add2(c[i].d,c[i].d);
			all+=c[i].d;
	}
	cout<<ans;
		return 0;
}

Lowest Common Ancestor

the lowest common ancestor (LCA) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest (i.e. deepest) node that has both v and w as descendants, where we define each node to be a descendant of itself (so if v has a direct connection from w, w is the lowest common ancestor).

Characteristics

• LCA(u)=u
• LCA(u,v)=u, if and only if u is the ancestor of v
• If u and v are not ancestor of each other, then they are separate in their lca’s son trees
• LCA(A$\bigcup$B)=LCA(LCA(A),LCA(B))
• u and v’s lea must be in the route from u to v(Shortest)

Realization

Easier way

Build a loop, and in the loop fInd the point which is deeper, and jump it to its father. When two points meet together, the poistion is their LCA.

Faster way

We premake a fa[x][i] array, and fa[x][i] Means the 2^i^ ancestor for point x. We can make fa[][]array through dfs.

int lca(int x,int y) {
	if(dep[x]<dep[y])swap(x,y);//Let's make sure x deeper
	for(int i=19; i>=0; i--) { //make x the same depth as y
	   if(dep[y]<=dep[anc[x][i]]) x=anc[x][i];
	}
	if(x==y) return x;//Base on charastic, we find the lca
	for(int i=19; i>=0; i--) { //Push up in the same time(If they are in the same depth)
	   if(anc[x][i]!=anc[y][i]) {
	      x=anc[x][i];
	      y=anc[y][i];
	    }
	}
	return anc[x][0];//It must be lca
}
void dfs(int x,int fa) {
  anc[x][0]=fa; //Default: set fa as x's father
	dep[x]=dep[fa]+1;
	for(int i=1; (1<<i)<=dep[x]; i++) { 
	  anc[x][i]=anc[anc[x][i-1]][i-1];//Calculate the ancestor 
	}
	for(int i=head[x]; i; i=node[i].next ) {
	   int j=node[i].d;
	   if(j!=fa) dfs(j, x);//Recursion
	}
}

The centroid of the tree

Defination

For a point in the tree, calculate its biggest son’s point number. For the point which has the smallest number. That should be the centroid.

Characteristics

• When the root is the centroid, every son’s scale won’t be larger than half of the whole tree
• When calculate the distance from every point to a single point, the centroid will be the smallest
• Conecting two trees through an edge, then the new centroid will be on the route that conect two centroids.

Realization

void getCentroid(int u, int fa) {
  siz[u] = 1;
  wt[u] = 0;
  for (int i = head[u]; ~i; i = nxt[i]) {
    int v = to[i];
    if (v != fa) {
      getCentroid(v, u);
      siz[u] += siz[v];
      wt[u] = max(wt[u], siz[v]);
    }
  }
  wt[u] = max(wt[u], n - siz[u]);
  if (rt == 0 || wt[u] < wt[rt]) rt = u;  // rt 为重心编号
}

So you might wonder how can we get size and father those kinds of information, and here is the most important method we are going to learn……

The alograthim I am going to talk about actually has no translation. So I just go with my Chinese……

接下来的内容没有英语翻译,所以我要开始说人话了

树链剖分

Concept

“树链” ，就是树上的路径。

“剖分”，就是把路径分类为重链和轻链。

常见的操作方式就是轻重剖分，这种方法能实现任意一点到根结点上的链的个数不超过logn条。

Method

记siz[v]表示以v为根的子树的节点数，dep[v]表示v的深度(根深度为1)，top[v]表示v所在的链的顶端节点，fa[v]表示v的父亲，son[v]表示与v在同一重链上的v的儿子节点（姑且称为重儿子）。 下图中圆圈内的数字表示树结点编号；加粗的边代表重链，反之则为轻链；树结点中带有小圆点的表示该条链所在链的顶端结点；

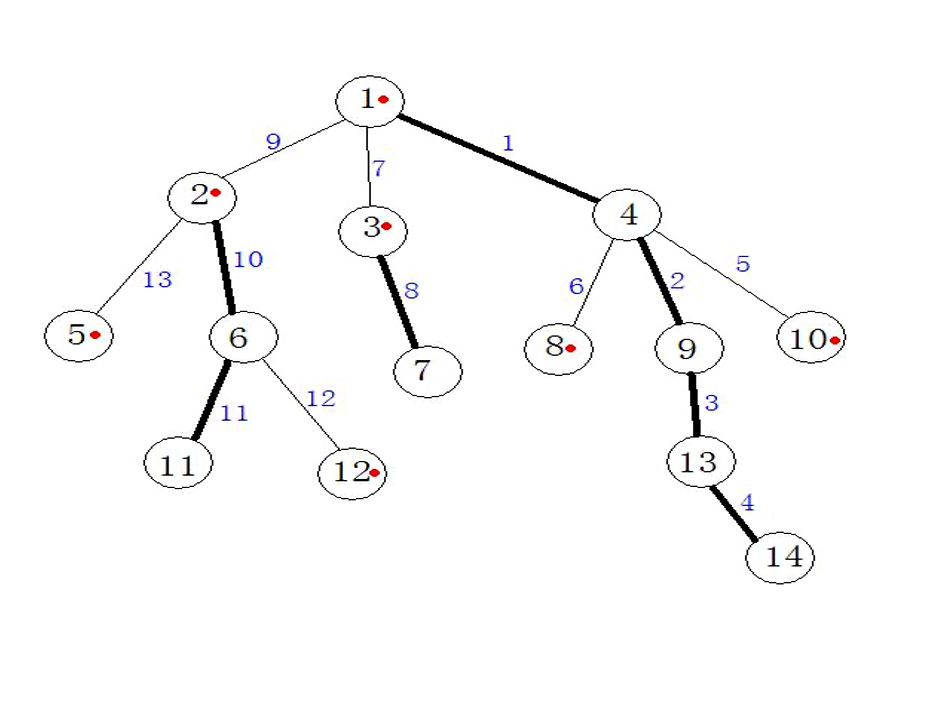
叫法

重儿子：siz[u]为v的子节点中siz值最大的，那么u就是v的重儿子。

轻儿子：v的其它子节点。

重边：点v与其重儿子的连边。

轻边：点v与其轻儿子的连边。

重链：由重边连成的路径。

轻链：轻边。

Charastics

• 如果(v,u)为轻边，则siz[u] * 2 < siz[v]

• 从根到某一点的路径上轻链、重链的个数都不大于logn

Realization

用两个dfs(可用bfs)来求出fa、dep、siz、son、top等信息；
dfs_1：

​ 把 fa、dep、siz、son求出来，比较简单，略过

dfs_2：

​ ⒈（重链）对于v，当son[v]存在（即v不是叶子节点）时，显然有top[son[v]] = topv。继续 dfs_2(son[v])；

​ ⒉（轻链）对于v的各个轻儿子u，显然有top[u] = u，进行dfs_2(u)过程。
这就求出了top。

这样就完成了轻重链划分，即树链剖分

void dfs1(int u){// siz、 son、 dep、fa
   siz[u]=1, son[u]=0;//记录顶点u的子节点个数及重儿子编号
   for(int i=head[u]; i; i=eg[i].next){
     int v=eg[i].d;
     if(v!=fa[u]){//避免绕回
        fa[v]=u;//v的父结点是u
        dep[v]=dep[u]+1;//v的深度=u的深度+1
        dfs1(v);//继续向下搜索
        siz[u]+=siz[v]; //u的儿子个数
        if(!son[u] || siz[v] > siz[son[u]]) //计算重儿子
           son[u]=v;
     }
   }
}
void dfs2(int u,int tp){//轻重链
	top[u]=tp;
	if(son[u])dfs2(son[u], tp);
	for(int i=head[u];i;i=eg[i].next){
		int v=eg[i].d;
		if(v!=fa[u]&&v!=son[u])dfs2(v,v);
	}
}

Seems to be long, but when we slow down and coding it few more times, it would be easy for us to learn.

例题

P3038 [USACO11DEC]Grass Planting G

题目描述

Farmer John has N barren pastures (2 <= N <= 100,000) connected by N-1 bidirectional roads, such that there is exactly one path between any two pastures. Bessie, a cow who loves her grazing time, often complains about how there is no grass on the roads between pastures. Farmer John loves Bessie very much, and today he is finally going to plant grass on the roads. He will do so using a procedure consisting of M steps (1 <= M <= 100,000).

At each step one of two things will happen:

• FJ will choose two pastures, and plant a patch of grass along each road in between the two pastures, or,
• Bessie will ask about how many patches of grass on a particular road, and Farmer John must answer her question.

Farmer John is a very poor counter – help him answer Bessie’s questions!

给出一棵n个节点的树，有m个操作，操作为将一条路径上的边权加一或询问某条边的权值。

输入格式

* Line 1: Two space-separated integers N and M

* Lines 2..N: Two space-separated integers describing the endpoints of a road.

* Lines N+1..N+M: Line i+1 describes step i. The first character of the line is either P or Q, which describes whether or not FJ is planting grass or simply querying. This is followed by two space-separated integers A_i and B_i (1 <= A_i, B_i <= N) which describe FJ’s action or query.

输出格式

* Lines 1..???: Each line has the answer to a query, appearing in the same order as the queries appear in the input.

输入输出样例

输入 #1

4 6 
1 4 
2 4 
3 4 
P 2 3 
P 1 3 
Q 3 4 
P 1 4 
Q 2 4 
Q 1 4

输出 #1

2 
1 
2

Solution

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int mx=1e5+5;
int n,m,w[mx],head[mx],num_edge;
struct Edge{
	int v,nxt;
}eg[mx<<1];
struct Node{
	int fa,son,dep,top,size,s,t;
}node[mx];
struct TREE{
	TREE *lson,*rson;
	int l,r,mid,len;
	int num,lazy;
}tree[mx<<2];
typedef TREE* Tree;
Tree Root,now_node=tree;
inline int read(){
	char c=getchar();int num=0;
	for(;!isdigit(c);c=getchar())
		if(c=='P') return 1;
		else if(c=='Q') return 2;
	for(;isdigit(c);c=getchar())
		num=num*10+c-'0';
	return num;
}

inline void add_edge(int u,int v){
	eg[++num_edge].v=v;
	eg[num_edge].nxt=head[u];
	head[u]=num_edge;
}

void dfs1(int u){
	node[u].size=1;
	for(int i=head[u],v;i;i=eg[i].nxt){
		v=eg[i].v;
		if(v==node[u].fa)
			continue;
		node[v].fa=u;
		node[v].dep=node[u].dep+1;
		dfs1(v);
		node[u].size+=node[v].size;
		if(node[v].size>node[node[u].son].size)
			node[u].son=v;
	}
}
int bound;
void dfs2(int u,int top){
	node[u].top=top;
	node[u].s=++bound;
	if(node[u].son){
		dfs2(node[u].son,top);
		for(int i=head[u],v;i;i=eg[i].nxt){
			v=eg[i].v;
			if(v==node[u].son||v==node[u].fa)
				continue;
			dfs2(v,v);
		}
	}
	node[u].t=bound;
}
void build(Tree &root,int l,int r){
	root=++now_node;
	root->l=l,root->r=r,root->mid=l+r>>1,root->len=r-l+1;
	if(l==r)return;
	build(root->lson,l,root->mid);
	build(root->rson,root->mid+1,r);
}

inline void pushdown(Tree root){
	if(root->lazy){
		root->lson->lazy+=root->lazy;
		root->rson->lazy+=root->lazy;
		root->lson->num+=root->lson->len*root->lazy;
		root->rson->num+=root->rson->len*root->lazy;
		root->lazy=0;
	}
}

void update(Tree root,int l,int r){
	if(root->l==l&&r==root->r){
		root->num+=root->len;
		root->lazy+=1;
		return;
	}
	pushdown(root);
	if(r<=root->mid)
		update(root->lson,l,r);
	else if(l>root->mid)
		update(root->rson,l,r);
	else{
		update(root->lson,l,root->mid);
		update(root->rson,root->mid+1,r);
	}
	root->num=root->lson->num+root->rson->num;
}

int query(Tree root,int l,int r){
	if(root->l==l&&root->r==r)
		return root->num;
	pushdown(root);
	if(r<=root->mid)
		return query(root->lson,l,r);
	else if(l>root->mid)
		return query(root->rson,l,r);
	else
		return query(root->lson,l,root->mid)+query(root->rson,root->mid+1,r);
}

inline void Modify(int x,int y){
	int fx=node[x].top,fy=node[y].top;
	while(fx!=fy){
		if(node[fx].dep>node[fy].dep){
			update(Root,node[fx].s,node[x].s);
			x=node[fx].fa;
			fx=node[x].top;
		}
		else{
			update(Root,node[fy].s,node[y].s);
			y=node[fy].fa;
			fy=node[y].top;
		}
	}
	if(x!=y){
		if(node[x].dep>node[y].dep)
			update(Root,node[y].s+1,node[x].s);
		else
			update(Root,node[x].s+1,node[y].s);
	}
}

inline int Query(int x,int y){
	int fx=node[x].top,fy=node[y].top;
	int ans=0;
	while(fx!=fy){
		if(node[fx].dep>node[fy].dep){
			ans+=query(Root,node[fx].s,node[x].s);
			x=node[fx].fa;
			fx=node[x].top;
		}
		else{
			ans+=query(Root,node[fy].s,node[y].s);
			y=node[fy].fa;
			fy=node[y].top;
		}
	}
	if(x!=y){
		if(node[x].dep>node[y].dep)
			return ans+query(Root,node[y].s+1,node[x].s);
		else
			return ans+query(Root,node[x].s+1,node[y].s);
	}
	return ans;
}

int opt,u,v;
int main(){
	n=read(),m=read();
	for(int i=1;i<n;++i){
		u=read(),v=read();
		add_edge(u,v);
		add_edge(v,u);
	}
	dfs1(1);
	dfs2(1,1);
	build(Root,1,n);
	for(int i=1;i<=m;++i){
		opt=read(),u=read(),v=read();
		if(opt==1)
			Modify(u,v);
		else
			printf("%d\n",Query(u,v));
	}
	return 0;
}