大脑与同构

[[同构与层次]]

同构也是本书最重要的概念之一，意为**保存信息的变换。两个同构的事物它们既有差异又有共同点，它们的结构可以相互映射，一个结构的部分在另一个中有相对应的部分，而且其对应的部分在总体结构中起着相似的作用

我们能认识事物的意义就是因为同构，对于同构的认识在人们脑海中产生了意义。通俗的讲我们看到一个新事物或接收到一条新消息时会把它跟经验里的旧事物做对比，以旧认新，当找到新旧的相似点，发现二者的同构关系时我们才能给新事物一个意义。所有的形式系统也因同构地反应了现实世界才有了意义。比如书主介绍的pq- 系统 ，它的定理长这样：
-p-q–
-p–q—
–p–q—-
我会把系统解释为加法，因为每一个符号都能找到准确的解释， 系统和现实世界的加法产生了同构。而同时我们脑中表示pq-系统的符号和过去经验中表示加法的符号发生了关系：

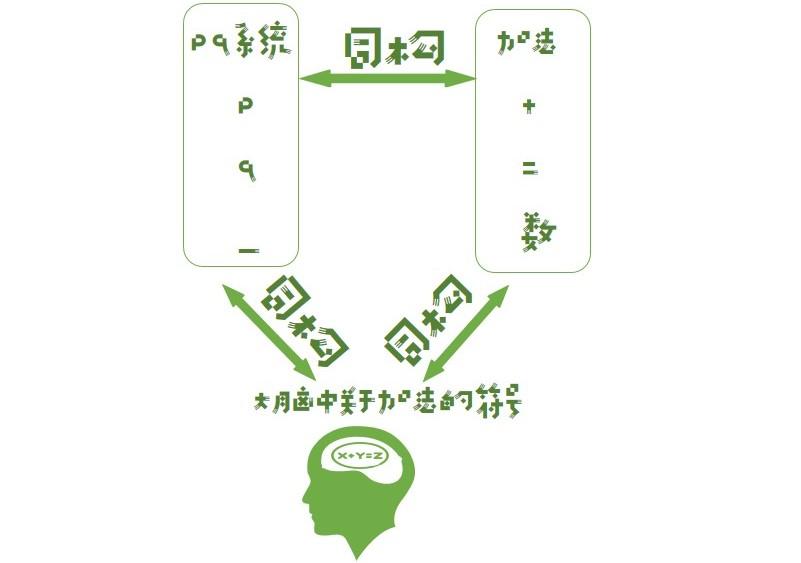
pq系统因和加法同构而有意义，它和加法同构是因为我们把它解释为加法。但你也可以把系统解释为其它东西，不同的解释可能产生不同的意义，但前提是要与这个系统存在某种同构关系（如果你把p解释为屁股，q解释为球，- 解释为树，这个系统是没法产生意义的），所以意义不止一种，一千个读者眼中有一千个哈姆雷特就是因为哈姆雷特在不同人脑中同构于不同的事物。

人类通过构造同构于世界的形式系统来认知世界 。物理学家用F=ma 来描述自然界的力，化学家用元素周期表反映物质组成，弗洛伊德用本我，自我，超我的模型解释心灵结构。人类认知世界的过程就是人类在各学科构造形式系统并用其中推演出的定理来描述世界现象的过程（这句话再出现一遍），这应该更能让你了解哥德尔定理的发现有多么重大的历史意义

这里还有个问题：世上所有的现象都能构建与之同构的形式系统吗？有没有在本质上毫无意义毫无规律的现象？

我们的直觉是有，因为根据经验，生活触手可及的地方都充斥着太多毫无意义的东西，但作者却偏向认为：世上没有毫无意义的消息，只是你没找到释读的系统罢了
作者用数列举例子：
7 8 5 3 9 8 1 6 3 3 9 7 4 4 8 ……
你可能会认这是毫无规律的随机数列，但实际上它是 pi/4的小数部分。这其实就说明自然界的一切现象，不管乍一看多混乱都有可能被形式化

我们可以认为现实世界只为我们提供现象，而发掘意义需要我们找到解释现象的形式系统
作者还有个充满决定论意味的猜想：从广义上看，现实世界本身就可以看成一个非常复杂的形式系统，他的符号不是写在二维的纸上，而是在三维空间里运动的粒子。如果真是这样，我们可以设想这个无比宏伟的系统的定理可以推出粒子在宇宙所有时期的所有布局！