线性代数

---

title: 线性代数
date: 2020-04-25 20:18:31
tags:
- 数学
categories: 技术
mathjax: true

概念

线性代数是代数学的一个分支，主要处理线性关系问题。线性关系意即数学对象之间的关系是以一次形式来表达的。

最重要的

标量

Scalar，单独数字，通常小写

s $\in$ R : 定义实数标量s

n $\in$ N: 定义整数标量

向量

Vector，有序的一列数，通过次序索引，可确定一个每个单独的数

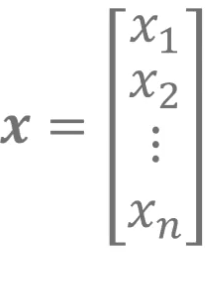
两向量相加遵循平行四边形法则

向量的模

$$a = [x_{1} + x_{2} + x_{3}…+x_{n}]$$

$$|a| = \sqrt{x_{1}^2 + x_{2}^2 + x_{3}^2…+x_{n}^2}$$

向量与标量

$$a = [x_{1} + x_{2} + x_{3}…+x_{n}]$$

• 向量与标量相加

s $\in$ R ，

$$ s+a=[s+x_{1},s+x_{2},s+x_{3},…s+x_{n}] $$

• 向量与标量相加

s $\in$ R ，

$$ sa=[sx_{1},sx_{2},sx_{3},…sx_{n}] $$

矩阵

[[01矩阵]]

Matrix是二维数组，每个元素由两个索引确定，通常为大写字母。

• A$\in R^{m*n}$,高度为m，宽度为n的实体矩阵
• $A_{ij}$第i行第j列的元素

形状一样的矩阵才能相加

$$C_{i,j}=A_{i,j}+B_{i,j}$$

矩阵加或乘标量都是每一项分别加或乘

行列式

[[02行列式]]

行列式是由一些数据排列成的方阵经过规定的计算方法而得到的一个数。当然，如果行列式中含有未知数，那么行列式就是一个多项式。它本质上代表一个数值。

一阶行列式

$$|a_{1}|=a_{1}$$

二阶行列式

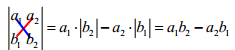
三阶行列式

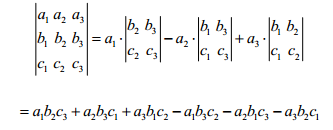
张量

（Tensor）三维的数组

矩阵运算

向量乘法

具有相同维度的向量，相乘得到一个标量

$$\overline{a}*\overline{b}=|a||b|cos\theta$$

矩阵与向量相乘

矩阵列数（竖）=向量行数（横）

结果行数=矩阵行数

D=np.diag([2,4,3,1])#创建对角矩阵
X=np.array([3,2,2,7])#创建向量
np.dot(D,X)#相乘
#得到array([6,8,6,7])

向量*矩阵=另一个向量（Application：解方程组（Creamer‘s rule））

Creamer’s rule

算四次行列式。。。

对于如下四元一次方程组：

$$a_{1}x_{1}+b_{1}x_{1}+c_{1}x_{3}+d_{1}x_{4}=e_{1}$$

$$a_{2}x_{1}+b_{2}x_{1}+c_{2}x_{3}+d_{2}x_{4}=e_{2}$$

$$a_{3}x_{1}+b_{3}x_{1}+c_{3}x_{3}+d_{3}x_{4}=e_{3}$$

$$a_{4}x_{1}+b_{4}x_{1}+c_{4}x_{3}+d_{4}x_{4}=e_{4}$$

设如下行列式：

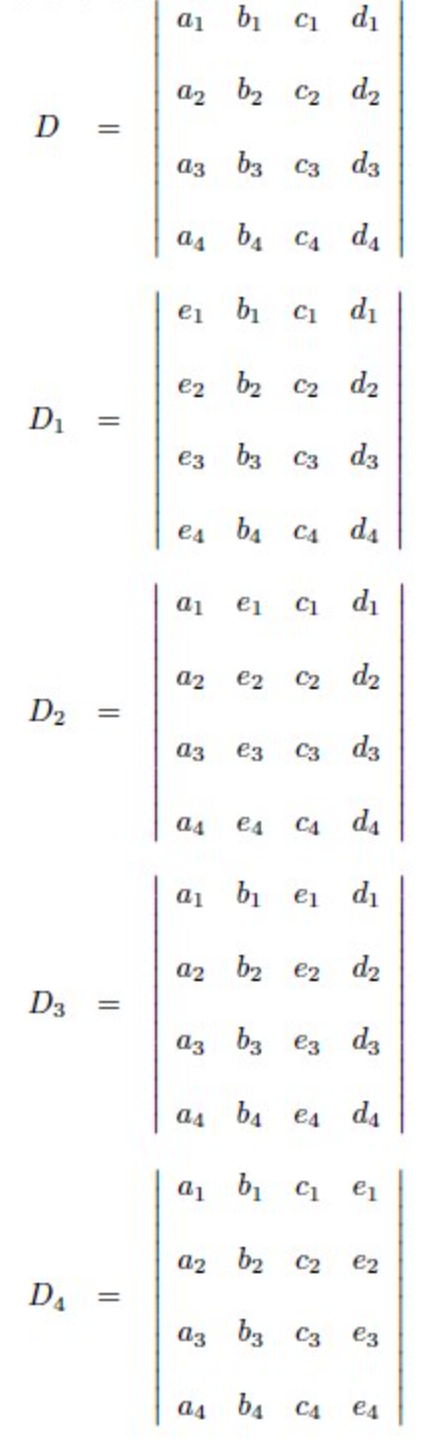
则原四元一次方程组的解为：

$$x_{1}=\cfrac{D_{1}}{D}$$

$$x_{2}=\cfrac{D_{2}}{D}$$

$$x_{3}=\cfrac{D_{3}}{D}$$

$$x_{4}=\cfrac{D_{4}}{D}$$

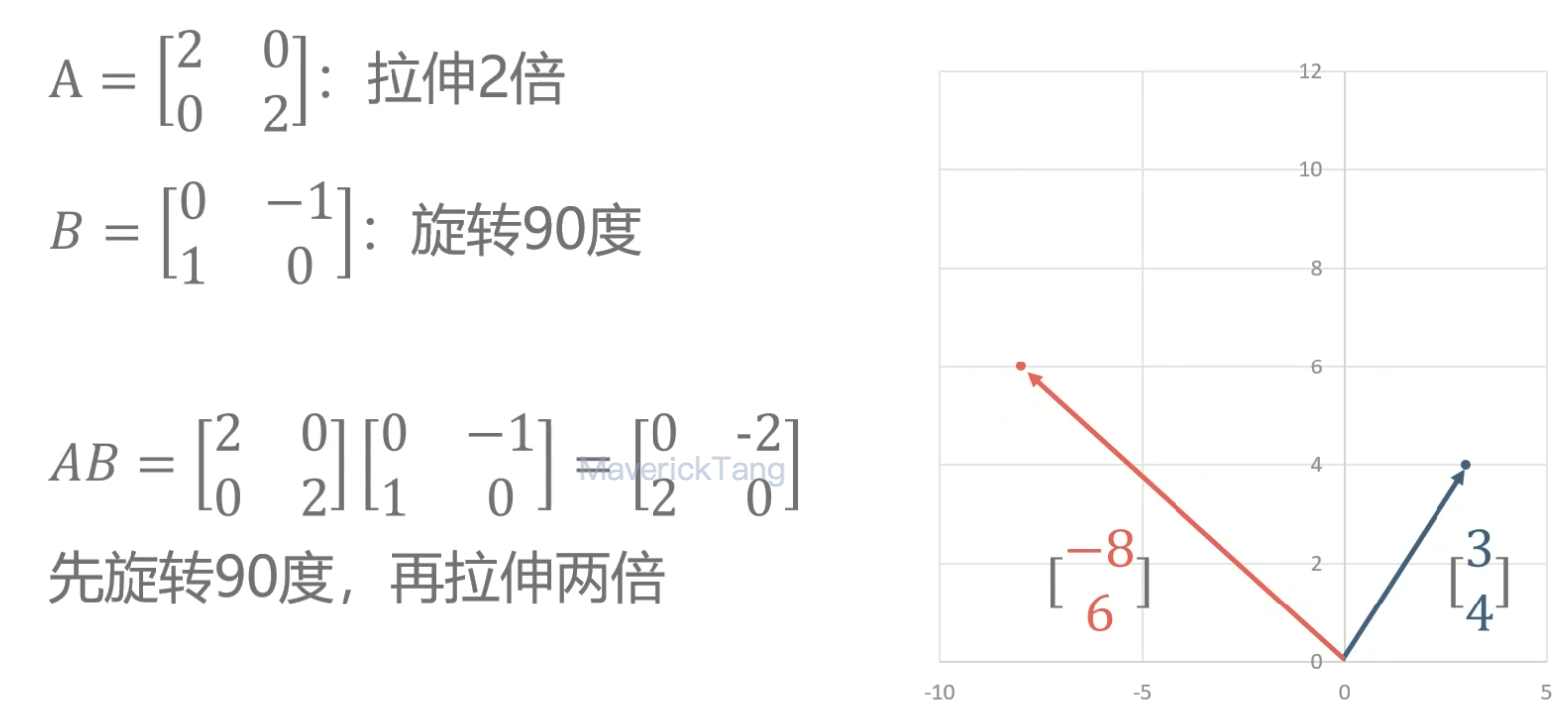
矩阵相乘

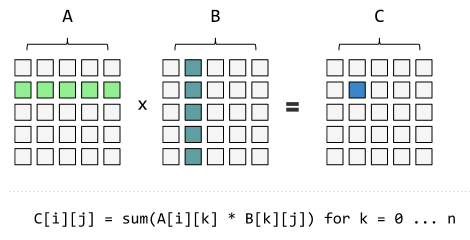
意义：

矩阵转置

Transpose：一对角线为轴的镜像

$$(A^{T})_{i,j}=A{j,i}$$

import numpy as np
A = np.array([6,4,24],[1,-9,8])
A.T

特殊矩阵

对角矩阵

除对角线外，其余元素皆为0的矩阵

python生成方法

np.diag([2,3,4])
#array([2,0,0]
#			[0,3,0]
#			[0,0,4])

对称矩阵

$$A=A^{T}$$

单位矩阵

Identity matrix，主对角线=1，其余位置元素为0

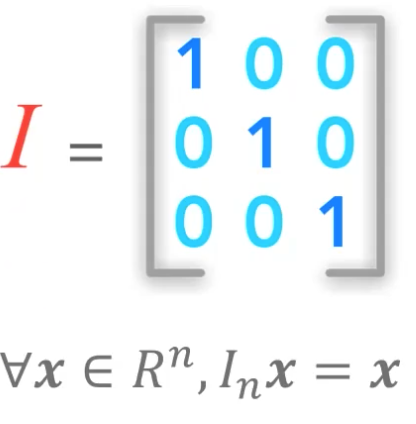
A*I=A

np.eye(3)#生成3*3的单位矩阵

逆矩阵

$$A*A^{-1}=I$$

逆矩阵需要:行数=列数

列向量之间线性无关

线性无关概念：

如果$$\overline{a}=x\overline{b}+y\overline{c}$$

则a是b，c的线性组合

如果在一组向量中，任意向量都不能表示为其他向量的线性组合

则该向量线性无关

求法（高斯消元）：

2X2

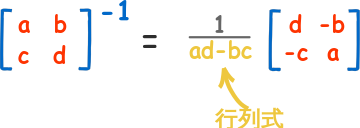
3X3(多X多)

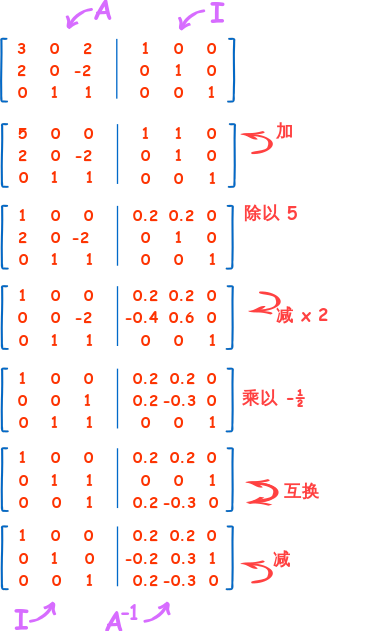
高斯－若尔当 方法

。。。。。。玩玩这些行 （加、乘或对换） 直至把矩阵 A 变成单位矩阵 I。

在单位矩阵上也做一模一样的运算， 单位矩阵便会奇妙的变成 逆矩阵！

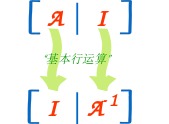
**”初等行运算”**是简单的运算，像把行相加，乘，对换位置。。。

Ex.

余子式、代数余子式和伴随

• 求余子式矩阵，
• 转成代数余子式矩阵，
• 转成伴随矩阵，
• 乘以 1/行列式。

一余子式

矩阵去掉使用在本行与本列的元素

$$M_{i,j}=$$

二求代数余子式

$$C_{i,j}=(-1)^{i+j}M_{i,j}$$

Ex.

三伴随

“转置” 以上的矩阵。。。。。。就是沿对角线对调元素的位置（在对角线上的元素不变）

Ex.

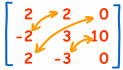
四乘以1/行列式

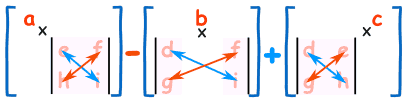
Python实现

A=np.array([1,3],[2,7])
A
np.linalg.inv(A)

[[03特征向量]]

[[04向量空间]]

[[05对称矩阵]]