C语言代码集

title: 代码集
date: 2020-03-29 19:35:14
tags:
- 竞赛
categories: 技术

简介

博主我隔离期间实在无聊于是无聊到整理代码模版

从入门到放弃

基础

输入类

读入优化

1
2
3
4
5
6
7
8
9
10
11
12
13
int rd(){
	int x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		x=x*10+c-'0';
		c=getchar();
	}
	return x*f;
}

高精度

高精度真的是mol鬼，到现在听到要打高精度觉得自己还是打不出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
struct bign {
	int len, s[mx];//高精度长度和存放数值
	bign() { memset(s,0,sizeof(s)),len=1;} //构造函数初始化
	bign (int num) { *this = num; }//低精度赋值
	bign (const char *num) { *this = num; } //字符串赋值
	bign operator = (const int num) {//低精度转换成高精度
		char st[mx]; sprintf(st,"%d",num);	return *this=st;
	}
	bign operator = (const char *num) {//将字符串转成高精度值
		len=strlen(num);
		for(int i=0; i<len; i++) s[i]=num[len-i-1]-'0';
		return *this;
	}
	void clean() {//清除高位 0
		while(len>1 && s[len-1]==0) len--;
	}
	bign operator + (const bign &b) { //重载运算符 +
		int l=max(len,b.len),i;
		bign c;
		for(i=0; i<l; i++) {
			c.s[i]+=(s[i]+b.s[i]);//当前位
			c.s[i+1]+=c.s[i]/10;//进位位
			c.s[i]%=10;//调整本位
		}
		c.len=l+1;
		c.clean();
		return c;
	}
	bign operator - (const bign &x) {//重载运算符-
		bign c=*this;
		for(int i=0; i<len; i++) {
			if(x.s[i]>c.s[i]) {
				c.s[i+1]--;//从前借一位
				c.s[i]+=10;//当前位加10
			}
			c.s[i]-=x.s[i];//直接减
		}
		c.clean();
		return c;
	}
	bign operator * (const bign &b) {//重载运算符*
		bign c;
		for(int i=0; i<len; i++) {
			for(int j=0; j<b.len; j++) {
				c.s[i+j]+=s[i]*b.s[j];//本位
				c.s[i+j+1]+=c.s[i+j]/10;//进位
				c.s[i+j]%=10;//调整本位
			}
		}
		c.len=len+b.len+1;
		c.clean();
		return c;
	}
	bign operator / (const bign &b) {
        bign c, f = 0;
        for(int i = len - 1; i >= 0; i--) {
            f =f*10;
            f.s[0] = s[i];
            while(f >= b) {
                f =f- b;
                c.s[i]++;
            }
        }
        c.len = len;
        c.clean();
        return c;
    }

	bool operator > (const bign &b) {//重载运算符 >
		if(len!=b.len) return len>b.len;
		for(int i=len-1; i>=0; i--) { //从高位开始对比
			if(s[i]!=b.s[i]) return s[i]>b.s[i];
		}
		return false;
	}
	bool operator < (const bign &b) {
		if(len!=b.len) return len<b.len;
		for(int i=len-1; i>=0; i--) {
			if(s[i]!=b.s[i]) return s[i]<b.s[i];
		}
		return false;
	}
	bool operator == (const bign &b) {
		return !(*this>b) && !(*this<b);
	}
	bool operator >= (const bign &b) {
		return *this>b || *this==b;
	}
	string str() const {//将高度精值转换成字符
		string re="";
		for(int i=0; i<len; i++) re=(char)(s[i]+'0')+re;
		return re;
	}
};
istream& operator >> (istream &in, bign &x) {//使高精度支持输入>>
	string s;
	in>>s;	x=s.c_str(); return in;
}
ostream& operator << (ostream &out, const bign &x) {//使高精度支持输出
	for(int i=x.len-1; i>=0; i--) out<<x.s[i];
}

排序

真香排序

不论会什么高级模版，总会想用它

1
2
3
4
bool cmp(int a,int b){
	return a<b;//从低到高
}
sort(a,a+n+1,cmp);

桶排

简单来说就是记录后找下标

1
2
3
4
5
6
7
8
9
10
int x,n;
	cin>>n;
	int a[100]= {0};
	for (int i=0; i<n; i++) {
		cin>>x;
		a[x]++;
	}
	for(int i=0; i<100; i++) 
		for(int m=1;m<=a[i];m++)
			cout<<i<<" ";

冒泡排序

相邻元素若不按照顺序则替换

1
2
3
4
5
6
7
8
9
10
void bubble_sort(int a[],int n){
    int i,j,t;
    for(i=1;i<=n;i++){
      for(j=i+1;j<=n;j++){
          if(a[i]<a[j]){
             swap(a[i],a[j]);
          }
      }
   }
}

归并排序

递归拆分子序列

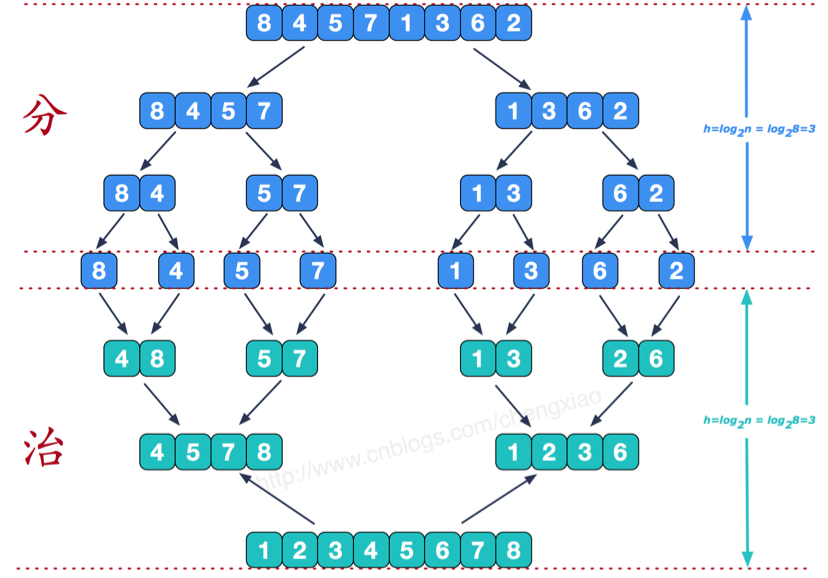
image-20200329201857057.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void merge_sort(int *a, int l, int r , int *t){//要排序数组a,起始l，终止r，暂存空间t
  if(r-l>1){    
       int m=(l+r)>>1;//中间进行划分
       int p=l, q=m, i= l;
   		 merge_sort(a,l,m,t);//划分
    	 merge_sort(a,m,r,t);//划分
       while(p<m ||q<r){         
         if(q>=r || (p<m && a[p]<a[q]))
              	t[i++] = a[p++];
              //将左则暂存至临时空间         
         else 
               t[i++] = a[q++];  
               //将右则暂存至临时空间	
       }
    for(i=l; i<r; i++)a[i]= t[i];
  }
}

快速排序

基本思想是通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的均比另一部分小,则可分别对这两部分记录继续进行排序,以达到整个序列有序.

假定待排序列为{r[s],r[s+1],…..r[t]},首先选取一个记录作为枢轴(pivot),然后按下述原则重新排列其余记录.

将所有较它小的记录安置在它之前,将所有较它大的记录安置在它之后.由此可见此”枢轴”记录最后所落的位置I作分界线,将原序列分割成两个{r[s],r[s+1],…r[i-1]}和{r[i],r[i+1],…r[t]}.这个过程称做一趟快速排序(或一次划分).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int part(int l, int r, int a[]) { 
    int p=a[l];
	while(l<r) {//保证没有重叠
		while(l<r && a[r]>=p) r--;
		a[l]=a[r];//将右边不适宜的数字放到左边
		while(l<r && a[l]<=p) l++;
		a[r]=a[l];
	}
	a[l]=p;
	return l;
}
void qsort(int l, int r, int a[]) {
	if(l<r) {
		int p=part(l,r,a);
		qsort(l,p,a);
		qsort(p+1,r,a);
	} 
}

排序对比

进制转换

1
2
3
4
5
6
7
8
9
10
11
void tenout(int x,int m){//十进制转任意进制
    while(x){a[++n]=x%m;x/=m;}
    for(int i=n;i>=1;--i)
        (a[i]<10)?(cout<<a[i]):(cout<<char(a[i]+('A'-10)));//如果小于10就直接输出，else输出字母
}

void getten(int x,char s[]){//任意进制转十进制
    ans=0;
    for(int i=0;i<strlen(s);i++) 
        ans=ans*x+(isdigit(s[i])?(s[i]^'0'):(s[i]-'A'+10));
}

提高

图论

默认存储及加边

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct Edge{
       int dest;//destination
       int val;//edge's value
       int next;//next edge
  }eg[mx*2];//mx is the numer of the edges, if it is undirected you need to double
int n,m;//nomber of point in the graph，number of edge in the graph 
int head[MAX]={0};//The head in the graph
int top=0;//The exact number of the edeges
void addedge(int u, int v, int val){ 
    eg[++top].dest=v;//v is the tail of the edge(destination)
    eg[top].val=val;//edge's value
    eg[top].next=head[u];//next edge's number
    head[u]=top;//Remeber this edge as another edge for the head u.
}

DFS

1
2
3
4
5
6
7
8
9
int vis[mx]={0};//To make sure you won't travel through the same edge over and over again
void dfs(int s){
	vis[s]=1;
	for(int i=head[s];i;i=eg[i].next){//travel
		if(!vis[eg[i].dest]){//haven't travel through
			dfs(eg[i].dest);//Then travel
		}
	}
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<queue>//Import queue libaray
queue<int>q;//Declare queue
void bfs(int s){
	q.push(s);vis[s]=1;//push s into the queue and vis
	while(!q.empty()){//As long as there is still elements in the queue
		int u=q.front();//Get the front of the queue
		q.pop();//Get the front of the queue out
		for(int i=head[u];i;i=eg[i].next){//Same old story
			int v=eg[i].dest;
			if(!vis[v]){
				q.push(v),vis[v]=1;
			}
		}
	}
}

Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
struct node{//Declare another struct to restore the information for the point
	int dis,pos;//pos means the number of the point
	bool operator <( const node &x )const{//declare the operator '<' by our own function
		return x.dis < dis;
	}
};
std::priority_queue<node> q;//priority queue
int dis[mx],vis[mx];
void dijkstra(int s){
	dis[s]=0;
	q.push((node){0,s});//push into queue as struct node
	while(!q.empty()){
		node tmp=q.top();q.pop();
		int x=tmp.pos,d=tmp.dis;
		if(!vis[x]){//Got to the tail, if we didn't visit it
		vis[x]=1;
		for(int i=head[x];i;i=eg[i].next){
			int y=eg[i].dest;
			if(dis[y]>dis[x]+eg[i].val){
				dis[y]=dis[x]+eg[i].val;//The core of the code, to replace for smaller
				if(!vis[y])//Got to the head, if we didn't visit it
					q.push((node){dis[y],y});
				}
			}
		}
	}
}

Floyd

1
2
3
4
5
6
7
8
9
10
void floyd(){
	for(int k=1;k<=n;k++) {
		for(int i=1; i<=n; i++) {
			for(int j=1; j<=n; j++) {
				if(g[i][k]<inf&&g[k][j]<inf&&g[i][j]>g[i][k]+g[k][j])
					g[i][j]=g[i][k]+g[k][j];
			}
		}
	}
}

SPFA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void spfa(int s){
	int u,v;    memset(dist,0x3f,sizeof(dist));//Initialize dist
	dist[s]=0;//Get start point as 0
	inque[s]=1;//Memorize the s is in the queue
	q.push(s);//in queue
	while(!q.empty()){
		u=q.front(), q.pop();  inque[u]=0;//Get the front of queue out
		for(int i=head[u]; i; i=eg[i].next){
			  v=eg[i].dest;
			  if(dist[v]>dist[u]+eg[i].val){//If find a route with smaller value
				  dist[v]= dist[u]+eg[i].val;//change it 
				  fa[v]=u;//Memorize the tail of v
				  if(!inque[v]){
					  q.push(v), inque[v]=1;
				  }
			  }
		}
	}
}

Difference between Dij+heap and SPFA!!!

Dij:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
while(!q.empty()){
  //If priority queue is not empty
		node tmp=q.top();q.pop();
  //get top out
		int x=tmp.pos,d=tmp.dis;
		if(!vis[x]){//Got to the tail, if we didn't visit it
		vis[x]=1;
		for(int i=head[x];i;i=eg[i].next){
			int y=eg[i].dest;
			if(dis[y]>dis[x]+eg[i].val){
        //Relax
				dis[y]=dis[x]+eg[i].val;//The core of the code, to replace for smaller
				if(!vis[y])//Got to the head, if we didn't visit it
					q.push((node){dis[y],y});
        //New distance and new point into the queue
				}
			}
		}
	}

SPFA:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
while(!q.empty()){
   //if regular queue is not empty
	u=q.front(), q.pop();  inque[u]=0;//Get the front of queue out
   //Get top out
   //And Remember!!!
	for(int i=head[u]; i; i=eg[i].next){
		  v=eg[i].dest;
		  if(dist[v]>dist[u]+eg[i].val){//If find a route with smaller value
         //Relax
			  dist[v]= dist[u]+eg[i].val;//change it 
			  fa[v]=u;//Memorize the tail of v
			  if(!inque[v]){
           //the points that are Relaxed but not in queue get into the queue
				  q.push(v), inque[v]=1;
			  }
		  }
	}
}

So the difference is clear enough:

Dji+heap: Small root pile, every time get the shortest distance, for this point, the shortest distance won’t change!

SPFA: Use queue. Get the front out of queue, might be renew in the future, it is won’t be always the same.

复杂度

Usage

Shortest-PathsProblem Sparse Graph Dense Graph With negative value
Single-Source Dijkstra+heap SPFA/Dijkstra+heap SPFA
APSP(Undirected graph) SPFA/Floyd SPFA SPFA
APSP(Directed graph) Floyd SPFA/Dijkstra+heap SPFA

​ APSP((All Pairs Shortest Path))

Complexity

Solving ways Time Complexity Space Complexity
Dijkstra+heap O(E*lgV) O(n^2)
SPFA O(kE) (Not stable) O(n)
Floyd O(n^3) O(n)

树论

线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include<iostream>
#include<cstdio>
#define MAX 100010
using namespace std;
typedef  unsigned long long ll;
struct Node {
	int l,r;//区间左右端点
	ll value;//区间和值
	ll add,time;//区间同时增加或乘一个数的延迟标记
};
Node tr[MAX<<2]= {0};
ll aa[MAX]= {0};
ll N,M,P;
ll Read() {
	ll x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9') {	if(c=='-')f=-1;	c=getchar(); }
	while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
	return x*f;
}
//初始化线段树
void build(int i,int l,int r) {
	tr[i].l=l,tr[i].r=r,tr[i].value=0,tr[i].time=1;
	if(l==r) {
		tr[i].value=aa[l];
		return;
	}
	build(i<<1,l,(l+r)>>1);//建立左子树区间
	build(i<<1|1,((l+r)>>1)+1,r);//建立右子树区间
	tr[i].value=tr[i<<1].value+tr[i<<1|1].value;//更新编号为i的区间和(由左右儿子来)
}
//向下更新
void pushdown(int i) {
	if(tr[i].add==0&&tr[i].time==1) return;//无需向下更新
	if( tr[i].l==tr[i].r ) {//避免访问无效内存(叶子没有儿子)
		tr[i].add=0;
		tr[i].time=1;
		return;
	}
	tr[i<<1].value=(tr[i<<1].value*tr[i].time+tr[i].add*(tr[i<<1].r-tr[i<<1].l+1))%P;
	//左儿子区间值
	tr[i<<1|1].value=(tr[i<<1|1].value*tr[i].time+tr[i].add*(tr[i<<1|1].r-tr[i<<1|1].l+1))%P;
	//右儿子区间值
	tr[i<<1].time=tr[i<<1].time*tr[i].time%P;//左儿子更新倍数
	tr[i<<1].add=(tr[i<<1].add*tr[i].time+tr[i].add)%P;//左儿子更新增加数
	tr[i<<1|1].time=tr[i<<1|1].time*tr[i].time%P;//右儿子更新倍数
	tr[i<<1|1].add=(tr[i<<1|1].add*tr[i].time+tr[i].add)%P;//右儿子更新增加数
	tr[i].add=0;//add延迟标记复0
	tr[i].time=1;//time倍增延迟标记恢复1
}
//区间求和 (区间查询)
ll query(int i,int l,int r) {
	if(l<=tr[i].l&&r>=tr[i].r) {//刚好罩着区间
		return tr[i].value;
	}
	if(l>tr[i].r||r<tr[i].l) return 0;//不相关区间
	pushdown(i);//向下更新延迟标记值
	return (query(i<<1,l,r)+query(i<<1|1,l,r));//返回左右儿子区间和值
}
//区间更新(将区间增加一个值k)
void updateadd(int i,int l,int r,int k) {
	pushdown(i);
	if(l<=tr[i].l&&r>=tr[i].r) {
		tr[i].value+=(tr[i].r-tr[i].l+1)*k%P;
		tr[i].add=k%P;
		return;
	}
	if(r<tr[i].l||l>tr[i].r) {
		return;
	}
	updateadd(i<<1,l,r,k);
	updateadd(i<<1|1,l,r,k);
	tr[i].value=(tr[i<<1].value+tr[i<<1|1].value)%P;
	return;
}
//区间更新(将区间每个值*上一个值k)
void updatetime(int i,int l,int r,int k) {
	pushdown(i);
	if(l<=tr[i].l&&r>=tr[i].r) {//此处对照区间增加一个值
		tr[i].value=tr[i].value*k%P;
		tr[i].time=k%P;
		return;
	}
	if(r<tr[i].l||l>tr[i].r) {
		return;
	}
	updatetime(i<<1,l,r,k);
	updatetime(i<<1|1,l,r,k);
	tr[i].value=(tr[i<<1].value+tr[i<<1|1].value)%P;
	return;
}
int main() {
	//freopen("data.txt","r",stdin);
	int i;
	int o,a,b,k;
	N=Read(),M=Read(),P=Read();
	for(i=1; i<=N; i++)	aa[i]=Read();
	build(1,1,N);//将数据离散到线段树上
	while(M--) {
		o=Read(),a=Read(),b=Read();
		if(o==1) {//区间倍增k
			k=Read();
			updatetime(1,a,b,k);
		}
		if(o==2) {//区间增加k
			k=Read();
			updateadd(1,a,b,k);
		}
		if(o==3) {//区间查询
			printf("%lld\n",query(1,a,b)%P);
		}
	}
	return 0;
}

树状数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int bit[mx+1], n;
int lowbit(int x){
   return x & -x;
}
int sum(int i){//Calculate the sum
  int s =0;
  while(i>0){
    s+=bit[i];  i-=lowbit(i);
  }
}
void add(int i, int x){//Add x to i
    while(i<=n){
       bit[i]+=x; i+=lowbit(i);
   }
}

重链剖分+lca

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<iostream>
#include<cstdio>
using namespace std;
int n,m,s;//分别表示树的结点个数、询问的个数和树根结点的序号
const int mx=500005;
struct Edge {
	int d;
	int w;
	int next;
} eg[mx<<1]= {0};
int dis[mx]={0};
int cnt=0,head[mx]= {0},dep[mx]= {0},siz[mx]= {0};
int son[mx]= {0},fa[mx]= {0},top[mx]= {0};
//增加边
int Read(){
	char c=getchar();
	int x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c<='9'&&c>='0') x=x*10+c-'0',c=getchar();
	return x;
}
void addEdge(int u,int v,int w) {
	eg[++cnt].d=v,eg[cnt].w=w,eg[cnt].next=head[u],head[u]=cnt;
}
void dfs1(int u) {
	siz[u]=1, son[u]=0;
	for( int i=head[u]; i; i=eg[i].next ) {
		int v=eg[i].d;
		if(v!=fa[u]) {
			dep[v]=dep[u]+1;
			fa[v]=u;
			dfs1(v);
			siz[u]+=siz[v];//计算儿子节点个数
			if(!son[u] || siz[v]>siz[son[u]]) son[u]=v;//记录重儿子结点编号
		}
	}
}
void dfs2(int u,int tp) {
	top[u]=tp;
	if(son[u]) dfs2(son[u],tp);//拉重链
	for( int i=head[u]; i; i=eg[i].next ) {
		int v=eg[i].d;
		if( v!=fa[u] && v!=son[u] ) dfs2(v,v);//拉轻链
	}
}
int lca(int x,int y) {	
    while(top[x]!=top[y]){
       if(dep[top[x]]>=dep[top[y]])	x=fa[top[x]];
       else y=fa[top[y]];
	}
	return dep[x]<dep[y]? x : y;
}
int main() {
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1; i<n; ++i) {
		int x,y; 
		x=Read(), y=Read();
		addEdge(x,y,0);
		addEdge(y,x,0);
	}
	dfs1(s);
	dfs2(s,s);
	for(int i=1; i<=m; ++i) {
		int x,y; 
		x=Read(), y=Read();
	    printf("%d\n",lca(x,y));
	}
	return 0;
}

离散化

离散化后只能知道数据之间的相对大小，但无法确定它们的真实值；

离散化的三个步骤：

1 sort排序

2 unique去重

3 lower_bound索引

1
2
3
4
5
6
7
8
for(int i=1; i<=n; i++){
    scanf("%d",&a[i]);
    b[i]=a[i];    //b[]是a[]的副本
}
sort(b+1,b+n+1);  //排序
int sum=unique(b+1,b+1+n)-b-1;  //去重
for(int i=1; i<=n; i++)
    a[i]=lower_bound(b+1,b+1+sum,a[i])-b;//索引

并查集

1
2
3
4
5
6
7
8
9
10
11
12
int set[mx];//集合
int find(int x){
  return x==set[x]?x:set[x]=find(set[x]);//到顶就return，没有就继续往上递归
}
void unionset(int x,int y){//合并集合
    int xx=find(x),yy=find(y);
    if(xx!=yy){
        if(xx>yy)swap(xx,yy);
        set[yy]=xx;
    }
}
 for(i=1;i<=n;i++)set[i]=i;//在主函数中初始化（各为一个集合）
程序 > 03高级语言 > C语言
#C语言代码集
C语言代码集
http://mavericreate.top/Blogs/2025/08/28/C语言代码集/
作者
唐浩天
发布于
2025年8月28日
许可协议