Matlab入门

matlab简介

  • help 在命令窗口（command windows）显示指定命令的简短使用说明
  • doc 以网页形式显示指定命令的帮助页，此命令显示的标准更加具体，还有各种使用举例
  • lookfor 按指定的关键词查询与之相关的命令
  • which 显示指定函数所在的目录. 例如
  • cd、dir、more
    1
    2
    3
    4
    1. help eig # 用于查看eig函数的帮助文档，查询结果在command窗口显示
    2. doc eig  # 同样是查看eig函数帮助文档，结果在单独的查看显示，比help显示更加完整详细
    3. lookfor eig # 模糊查找， 比如说你知道某个可能的函数是plo***， 但是你有记不清就可以用这个命令了
    4. which eig #查找函数具体在什么位置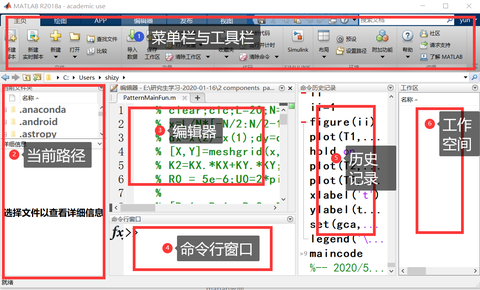

Matlab 变量

变量命名原则：以字母或者下划线开头(很少用下划线打头啊)；后面可以跟字母、数字和下划线；变量名区分字母的大小写.

Matlab 语句的通常形式

1
变量 = 表达式;

表达式是用运算符将有关运算量连接起来的式子，其结果被赋给赋值号“=”左边的变量

分号和续行符的作用

  • 若不想在命令行窗口的屏幕上输出结果，可以在语句最后加分号；
  • 如果语句很长，可用续行符 “…”（三个点）续行； 续行符的前面最好留一个空格.
    1
    2
    3
    4
    a = 1  % a=1就会在命令行窗口输出
    b = 1;  % 加了分号就不显示在命令行窗口
    c = 123+456+789+ ...
        123456  %三个点换行

变量的查询

  • who 显示工作空间中的所有变量；whos 查看工作空间中变量的详细属性
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    >> a = 1;
    b = 2;
    >> c = pi;
    >> who
    您的变量为:
    a  b  c  
    >> whos
      Name      Size            Bytes  Class     Attributes

      a         1x1                 8  double              
      b         1x1                 8  double              
      c         1x1                 8  double

系统预定义变量

  • pi ： 圆周率 π ；inf, Inf ：无穷大；nan, NaN ：Not-a-Number，一个不定值，如 0/0；eps ：浮点运算相对精度
  • i, j ：虚部单位, 通常为了避免混淆我们写作1i, 1j
  • 特殊变量 ans – 应尽量避免给系统预定义变量重新赋值

数学运算符

  • 加法；- 减法；* 乘法；/ 和 \ 除法（右左除）:^ 幂运算；
    点乘 (.*) 与点除 (./ ): 这两个用的特别多，例如
    1
    2
    3
    4
    5
    x  = [1 2 3];
    y  = [ 2 4 6];
    x.*y  % 输出1*2   2*4  3*6
    y./x %输出  2/1  4/2 6/3
    x.^3 %输出  1^3  2^3  3^3

/（向右倒称为右除） 右除 AB=C A=C/B
\（向左倒称为左除） 左除 AB=C B=A\C

运算符 目的
+ 加; 加法运算符。
- 减; 减法运算符。
***** 标量和矩阵乘法运算符。
.* 数组乘法运算符。
^ 标量和矩阵求幂运算符。
.^ 数组求幂运算符。
\ 左除法运算符。
/ 右除法运算符。
``.` 数组左除法运算符。
./ 数组右除法运算符。
: 冒号；生成规则间距的元素并表示整行或整列。
( ) 圆括号；封闭函数参数和数组索引；重写优先级。
[ ] 括号；附件数组元素。
. 小数点。
… 省略号；行连续运算符
, 逗号；分隔一行中的语句和元素
; 分号; 分隔列并抑制显示。
% 百分号；指定注释并指定格式。
_ 引用符号和转置运算符。
._ Nonconjugated转置运算符。
= 赋值运算符。

特殊变量与常量

名称 意义
ans 最近计算的答案。
eps 浮点精度。
i,j 虚数单位√-1。
Inf 无穷。
NaN 未定义的数值结果（不是数字）。
pi π

命令分隔符：逗号和分号

输出格式

Matlab 以双精度执行所有的运算，运算结果可以在屏幕上输出，同时赋给指定变量；若无指定变量，则系统会自动将结果赋给变量 “ans”；Matlab 中数的输出格式可以通过 format 命令指定；format 只改变变量的输出格式，但不会影响变量的值！

石头：matlab入门2：变量与赋值，数据保存于读取9 赞同 · 2 评论文章

format命令

默认情况下，MATLAB显示带有四个小数位值的数字。这就是所谓的short format。

但是，如果要提高精度，则需要使用format命令。

format long命令在小数点后显示16位数字。

窗口命令

用于管理会话的命令

命令 目的
clc 清除命令窗口。
clear 从内存中删除变量。
exist 检查文件或变量的存在。
global 声明变量为全局变量。
help 搜索帮助主题。
lookfor 在帮助条目中搜索关键字。
quit 停止MATLAB。
who 列出当前变量。
whos 列出当前变量（长显示）。

变量的存储

save 文件名 变量名列表

1
2
3
save  'file1.mat' p q %将变量 p与去存储到文件file1.mat里面

save('file1.mat','p','q') %和上面结果一样
  • 变量名列表中各变量之间用空格分隔

save命令用于将工作空间中的所有变量保存为当前目录中扩展名为.mat的文件。

例如，

1
save myfile

您以后可以随时使用load命令重新加载文件。

1
load myfile
  • 清除当前工作空间中的变量；
    1
    2
    3
    clear A  x   %清除指定的变量

    clear  all % 清除所有工作空间变量

查看变量

who命令显示您已使用的所有变量名。

1
who

MATLAB将执行上述语句并返回以下结果-

1
2
Your variables are:
a    ans  b    c

whos命令显示了有关变量的更多信息-

  • 当前内存中的变量
  • 每个变量的类型
  • 分配给每个变量的内存
  • 它们是否为复杂变量
1
whos

MATLAB将执行上述语句并返回以下结果-

1
2
3
4
5
6
7
8
Attr Name        Size        Bytes      Class
==== ====        ====        ====       ===== 
   a             1x1           8        double
   ans           1x70         757        cell
   b             1x1           8        double
   c             1x1           8        double

Total is 73 elements using 781 bytes

该clear命令variable(s)从内存中删除所有（或指定的）。

1
2
3
clear x     % it will delete x, won't display anything
clear       % it will delete all variables in the workspace
            %  peacefully and unobtrusively

用于系统的命令

MATLAB提供了各种有用的命令来处理系统，例如将当前工作作为文件保存在工作区中，并在以后加载文件。

它还为其他与系统相关的活动提供各种命令，例如显示日期，在目录中列出文件，显示当前目录等。

下表显示了一些常用的与系统相关的命令-

命令 目的
cd 更改当前目录。
date 显示当前日期。
delete 删除文件。
diary 开启/关闭日记文件录制。
dir 列出当前目录中的所有文件。
load 从文件加载工作区变量。
path 显示搜索路径。
pwd 显示当前目录。
save 将工作空间变量保存在文件中。
type 显示文件的内容。
what 列出当前目录中的所有MATLAB文件。
wklread 读取.wk1电子表格文件。

输入和输出命令

MATLAB提供以下与输入和输出相关的命令-

命令 目的
disp 显示数组或字符串的内容。
fscanf 从文件中读取格式化的数据。
format 控制屏幕显示格式。
fprintf 执行对屏幕或文件的格式化写入。
input 显示提示并等待输入。
; 禁止丝网印刷。

fscanf和fprintf命令的行为像C的scanf和printf函数。它们支持以下格式代码-

格式代码 目的
%s 格式化为字符串。
%d 格式化为整数。
%f 格式化为浮点值。
%e 以科学计数形式格式化为浮点值。
%g 以最紧凑的格式进行格式化：％f或％e。
\n 在输出字符串中插入新行。
\t 在输出字符串中插入一个选项卡。

格式函数具有以下用于数字显示的形式-

格式功能 最多显示
format short 四个小数位(默认值)。
format long 16位小数。
format short e 五位数加指数。
format long e 16位数字加指数。
format bank 两个小数位数。定点货币形式
format + 正数，负数或零。
format rat 有理近似。小数分数表示
format compact 禁止某些换行符。
format loose 重置为不太紧凑的显示模式。

向量，矩阵和数组命令

下表显示了用于处理数组，矩阵和向量的各种命令-

命令 目的
cat 连接数组。
find 查找非零元素的索引。
length 计算元素数。
linspace 创建规则间隔的矢量。
logspace 创建对数间隔的向量。
max 返回最大元素。
min 返回最小的元素。
prod 每列的乘积。
reshape 更改大小。
size 计算数组大小。
sort 对每一列进行排序。
sum 对每列求和。
eye 创建一个单位矩阵。
ones 创建一个数组。
zeros 创建一个零数组。
cross 计算矩阵叉积。
dot 计算矩阵点积。
det 计算数组的行列式。
inv 计算矩阵的逆。
pinv 计算矩阵的伪逆。
rank 计算矩阵的秩。
rref 计算精简行梯形表格。
cell 创建单元格数组。
celldisp 显示单元格数组。
cellplot 显示单元格数组的图形表示形式。
num2cell 将数字数组转换为单元格数组。
deal 匹配输入和输出列表。
iscell 标识单元格数组。

绘图命令

MATLAB提供了许多用于绘制图形的命令。下表显示了一些常用的绘图命令-

命令 目的
axis 设置轴限制。
fplot 函数的智能绘图。
grid 显示网格线。
plot 生成xy图。
print 打印图或将图保存到文件中。
title 将文本放在图的顶部。
xlabel 在x轴上添加文本标签。
ylabel 将文本标签添加到y轴。
axes 创建轴对象。
close 关闭当前图。
close all 关闭所有地块。
figure 打开一个新的图形窗口。
gtext 通过鼠标启用标签放置。
hold 冻结当前图。
legend 用鼠标放置图例。
refresh 重新绘制当前图形窗口。
set 指定对象（例如轴）的属性。
subplot 在子窗口中创建图。
text 在图中放置字符串。
bar 创建条形图。
loglog 创建对数-对数图。
polar 创建极坐标图。
semilogx 创建半对数图。（对数横坐标）。
semilogy 创建半对数图。（对数纵坐标）。
stairs 创建楼梯图。
stem 创建茎图。

几个小技巧

  • Matlab的命令记忆功能：上下箭头键(先输入命令的前几个字符，再按上下键缩小搜索范围)
  • 命令补全功能： Tab键 ；用 Esc键 删除命令行

矩阵

创建矩阵

Matlab 的操作对象是矩阵

  • 定义矩阵：直接输入法
    1
    2
    3
    4
    5
    A = [1  2  3; 4  5  6; 7  8  9]
    %或者
    A = [1  2  3; 
         4  5  6; 
         7  8  9]
  • 矩阵用方括号 “[ ]” 括起
    1
    mat = [元素]
  • 矩阵同一行中的元素之间用 空格 或 逗号 分隔
    1
    2
    mat1 = [1 2 3]; 
    mat2 = [1,2,3];%两者意义一样
  • 矩阵行与行之间用 分号 分开
    1
    mat3 =[ 1 2 3; 4, 5, 6];
  • 直接输入法中，分号可以用 回车 代替
    1
    2
    mat4 = [1 2 3
            4 5 6];
  • 利用函数建立数值矩阵：MATLAB提供了许多生成和操作矩阵的函数。例如: reshape 函数和 diag 函数等。reshape函数用于建立数值矩阵。diag函数用于产生对角阵。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>> x = 1:12
x =
     1     2     3     4     5     6     7     8     9    10    11    12
>> y = reshape(x,3,4) % reshape用法
y =
     1     4     7    10
     2     5     8    11
     3     6     9    12

>> z = 1:4
z =
     1     2     3     4
>> diag(z)   % 创建对角矩阵
ans =
     1     0     0     0
     0     2     0     0
     0     0     3     0
     0     0     0     4

转置

转置操作将列向量更改为行向量，反之亦然。转置操作由单引号（’）表示。

1
A=A';

建立矩阵的函数

1
2
3
4
5
6
7
eye(size(A))      % 产生与A矩阵同阶的单位矩阵
zeros(m,n)        % 产生0矩阵
ones(m,n)         % 产生幺矩阵
rand (m,n)        % 产生随机元素的矩阵
size(a)           % 返回包含两个元素的向量。
length(a)         % 返回向量的长度。 
inv(a)						% 求逆矩阵

赋值操作

  • 矩阵A是一个1X2矩阵，第一个元素1，第二个元素2
    1
    2
    A(1)=1;
    A(2)=2;
  • 大矩阵可以把小矩阵作为其元素
    1
    A = [A ; 3 4];

矩阵元素提取引用操作

单个元素的引用；利用小括弧和元素所在的位置(下标)
A(1) 引用A的第一个元素；
A(i)：向量 A 中的第 i 个元素；
A(i,j)：矩阵 A 中的第 i 行，第 j 列元素；多个元素的引用：
冒号的特殊用法；a:b:c %产生一个由等差序列组成的向量； a 是首项，b 是公差，c 确定最后一项；若 b=1，则 b 可以省略。

1
2
3
x=1:2:5;
x = 2:5; %省略
x = 10:-3:2;

矩阵元素的引用
A(i:j, m:n) 表示由矩阵 A 的第 i 到第 j 行和第 m 到第 n 列交叉线上的元素组成的子矩阵。可利用冒号提取矩阵的整行或整列

1
2
3
A(1, :)
A(:, 1:3)
A(:, :)

MATLAB 向量操作

MATLAB 向量追加

MATLAB 允许您将向量附加到一起来创建新的向量。

如果您有两个包含n和m个元素的行向量r1和r2，则要创建一个包含n个元素和m个元素的行向量r，通过添加这些向量，您可以编写-

1
r = [r1,r2]

您还可以通过添加这两个向量来创建矩阵r，向量r2将是矩阵的第二行-

1
r = [r1;r2]

数组运算

（1） 数组的加和减 （2） 数组的乘和除 （3） 数组的乘方

石头：matlab入门4：基本运算19 赞同 · 0 评论文章

1、行列式计算；

1
det([1 2 ;3 4])

2、求解线性方程组；

1
x = A\b

3、解特征值问题

1
eig(A)

数据类型

MATLAB 不需要任何类型声明或维度语句。每当 MATLAB 遇到一个新的变量名，它就创建变量并分配适当的内存空间。

如果变量已经存在，那么MATLAB将用新内容替换原始内容，并在必要时分配新的存储空间。

例如，

1
Total = 42

上面的语句创建一个名为“ Total”的1比1矩阵，并将值42存储在其中。

数据类型转换

MATLAB提供了用于将值从一种数据类型转换为另一种数据的各种函数。下表显示了数据类型转换函数-

函数 作用
char 转换为字符数组（字符串）
int2str 将整数数据转换为字符串
mat2str 将矩阵转换为字符串
num2str 将数字转换为字符串
str2double 将字符串转换为双精度值
str2num 将字符串转换为数字
native2unicode 将数字字节转换为 Unicode 字符
unicode2native 将Unicode字符转换为数字字节
base2dec 将N进制数字符串转换为十进制数
bin2dec 将二进制数字符串转换为十进制数
dec2base 将十进制数转换为字符串中的N进制数
dec2bin 将十进制转换为字符串中的二进制数
dec2hex 将字符串中的十进制数转换为十六进制数
hex2dec 将十六进制数字字符串转换为十进制数字
hex2num 将十六进制数字字符串转换为双精度数字
num2hex 将单精度和双精度转换为IEEE十六进制字符串
cell2mat 将单元格数组转换为数值数组
cell2struct 将单元数组转换为结构数组
cellstr 从字符数组创建字符串的单元格数组
mat2cell 将数组转换为单元格大小可能不同的单元格
num2cell 将数组转换为大小一致的单元格数组
struct2cell 将结构转换为单元格数组

数据类型的确定

MATLAB提供了各种功能来识别变量的数据类型。

下表提供了确定变量的数据类型的功能-

函数 作用
is 检测状态
isa 确定输入是否为指定类的对象
iscell 确定输入是否为单元格数组
iscellstr 确定输入是否为字符串的单元格数组
ischar 确定项目是否为字符数组
isfield 确定输入是否为结构数组字段
isfloat 确定输入是否为浮点数组
ishghandle 适用于处理图形对象句柄
isinteger 确定输入是否为整数数组
isjava 确定输入是否为Java对象
islogical 确定输入是否为逻辑数组
isnumeric 确定输入是否为数值数组
isobject 确定输入是否为MATLAB对象
isreal 检查输入是否为实数数组
isscalar 确定输入是否为标量
isstr 确定输入是否为字符数组
isstruct 确定输入是否为结构数组
isvector 确定输入是否为向量
class 确定对象的类别
validateattributes 检查数组的有效性
whos 列出工作空间中的变量，包括大小和类型

位运算

按位运算

按位运算符对位进行运算并执行逐位运算。＆，|和^的真值表如下-

p q p＆q p | q p ^ Q
0 0 0 0 0
0 1 0 1 1
1 1 1 1 0
1 0 0 1 1
函数 作用
bitand(a, b) 整数 a 和 b 的位与
bitcmp(a) a的逐位补码
bitget(a,pos) 在整数数组a的指定位置获取位
bitor(a, b) 整数a和b的位或
bitset(a, pos) 将bit设置为a的特定位置pos
bitshift(a, k) 返回一个由向左移动ķ比特，相当于乘以2 ķ。k的负值对应于右移位或除以2 | k | 并朝负无穷大四舍五入到最接近的整数。任何溢出位都将被截断。
bitxor(a, b) 整数 a 和 b 的位异或
swapbytes 整数 a 和 b 的位异或

冒号表示法

colon(:)是在MATLAB中最有用的运算符之一。它用于创建向量，下标数组和指定迭代。

如果要创建包含1到10的整数的行向量，请编写-

示例

1
1:10

MATLAB执行该语句并返回包含1到10的整数的行向量-

1
2
3
ans =                                                                           
                                                                                
   1    2    3    4    5    6    7    8    9   10

如果要指定一个增量值而不是一个值，例如-

示例

1
100: -5: 50

MATLAB执行该语句并返回以下结果-

1
2
ans =
   100    95    90    85    80    75    70    65    60    55    50

可以使用冒号运算符创建索引向量，以选择行，列或数组元素。

下表描述了它的用途（让我们有一个矩阵A）-

格式 目的
A(:,j) 是A的第j列。
A(i,:) 是A的第i行。
A(:,:) 是等效的二维数组。对于矩阵，这与A相同。
A(j:k) is A(j), A(j+1),…,A(k).
A(:,j:k) 是A（：，j），A（：，j + 1），…，A（：，k）。
A(:,:,k) 是第k个三维阵列A的页
A(i,j,k,:) 是三维数组A中的向量。向量包括A(i,j,k,1)，A(i,j,k,2)，A(i,j,k,3)等。
A(:) 是A的所有元素，被视为一个单独的列。在赋值语句的左侧，A（:)填充了A，并保留了之前的形状。在这种情况下，右侧必须包含与A相同数量的元素。

matlab图像可视化

二维平面图形与坐标系

  1. 线性坐标曲线 plot 函数命令，它可以生成线段、曲线和参数方程曲线的函数图形。命令格式: plot(X,Y) ; plot(x1,y1,x2,y2,…)
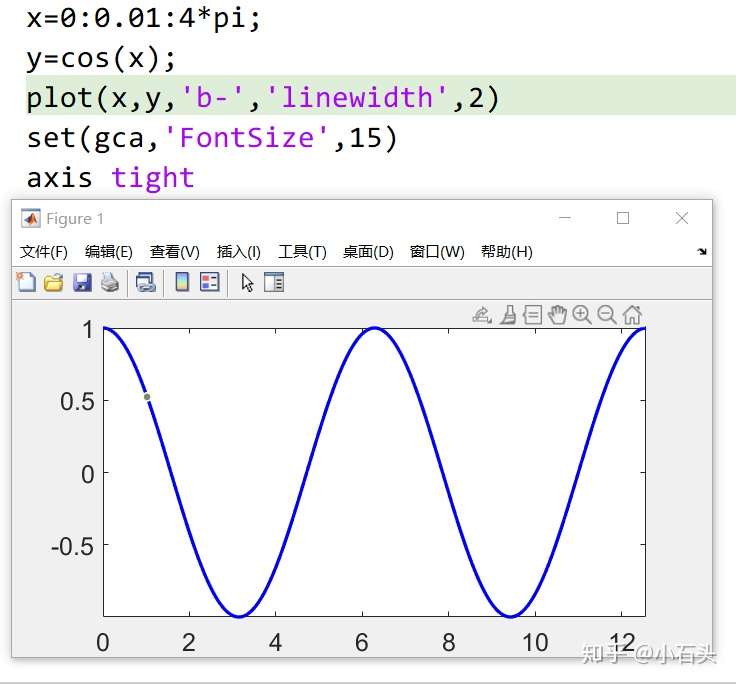
  2. 用命令 plot(x,y)绘制 y=cos(x)在一个周期内的图形。
1
2
3
x=0:0.01:2*pi;   
y=cos(x);   
plot(x,y)

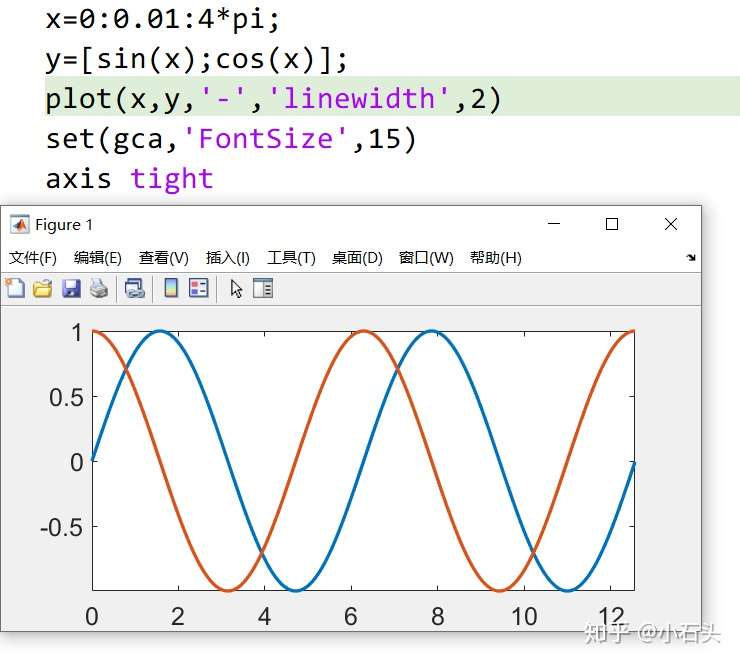
  1. 在同一图形窗口中用命令 plot(x,y)绘出正弦余弦函数的图形。
1
2
3
x=0:0.01:2*pi;   
y=[sin(x);cos(x)];   
plot(x,y)

  1. plot 函数可以设置曲线的线段类型、定点标记和线段颜色。 调用格式：plot(x,y,s) ，s 为类型说明参数，是字符串。 s 字符串可以是三种类型的符号之一，也可以是线型与颜色和定点标记与颜色的组合。用 hold on 命令在一个坐标系中增加新的图形对象。
  • 图形窗口的分割: 实现在同一个窗口中同时显示多个图像的命令subplot。 使用格式为：
1
subplot(m，n，i)

其含义为 ：把图形窗口分割为 m 行 n 列子窗口，然后选定第 i 个窗口为当前窗口。 subplot 命令不仅用于二维图形，对三维图形一样适用。其本质是将 figure 窗口分为几个区域，再在每个区域内分别绘图。

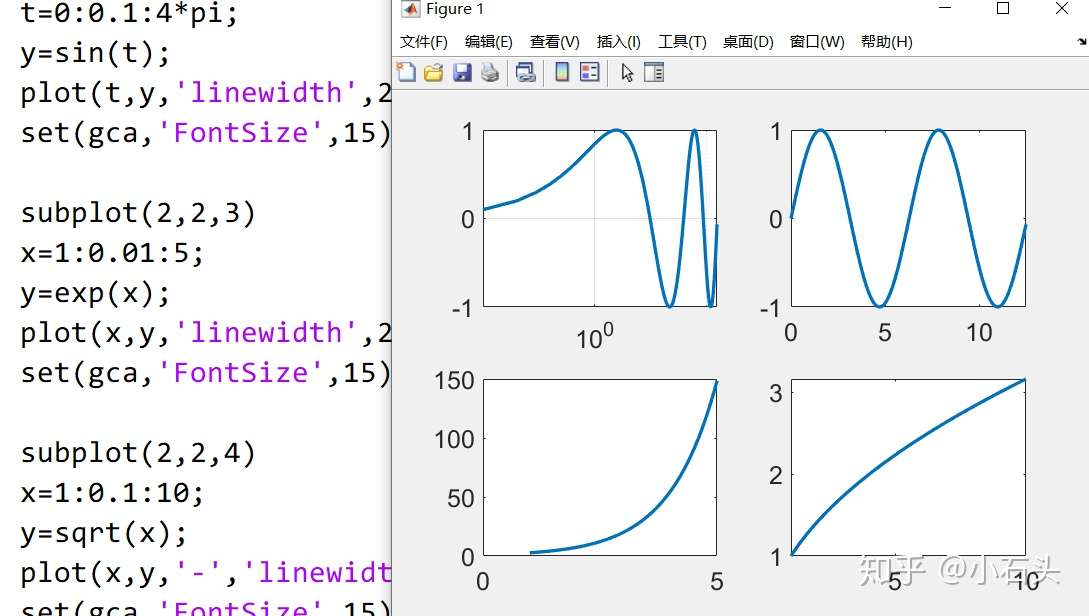
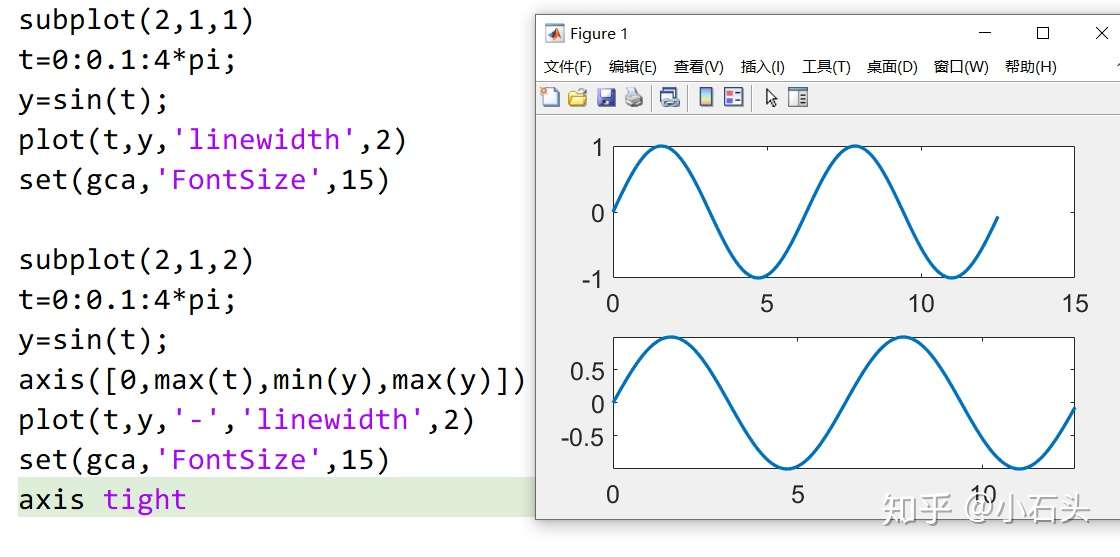
  • 用 subplot 函数把两种不同的图形综合在一个图形窗口中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
subplot(2,2,1)
t=0.1:0.1:4*pi;
y=sin(t);
semilogx(t,y,'linewidth',2)
grid on
set(gca,'FontSize',15)

subplot(2,2,2)
t=0:0.1:4*pi;
y=sin(t);
plot(t,y,'linewidth',2)
set(gca,'FontSize',15)

subplot(2,2,3)
x=1:0.01:5;
y=exp(x);
plot(x,y,'linewidth',2)
set(gca,'FontSize',15)

subplot(2,2,4)
x=1:0.1:10;
y=sqrt(x);
plot(x,y,'-','linewidth',2)
set(gca,'FontSize',15)
axis tight

  1. 坐标系的调整 实现坐标系的调整的命令是 axis 函数。 调用格式为：axis([xmin,xmax,ymin,ymax,zmin,zmax])
    坐标的最小值（ xmin,ymin,zmin）必须小于相应的最大值（ xmax,ymax,zmax）.
1
2
3
4
5
6
7
8
9
subplot(2,1,1) 
t=0:0.1:4*pi; 
y=sin(t); 
plot(t,y)  
subplot(2,1,2) 
t=0:0.1:4*pi; 
y=sin(t); 
plot(t,y) 
axis([0,max(t),min(y),max(y)])

三维绘图

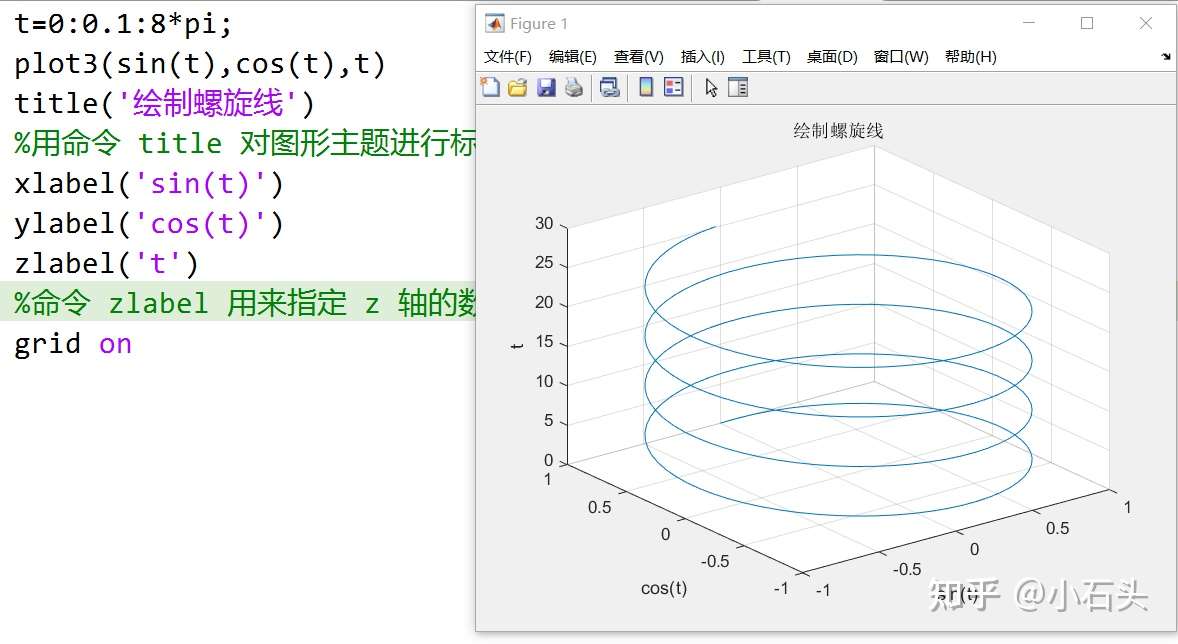
绘图命令 plot3. 其调用格式为：plot3(X1,Y1,Z1,s1,X2,Y2,Z2,s2,…)

参数的含义如下： X1, Y1,Z1：第一到三维数据，是尺寸相等的向量/矩阵； s、s1、s2：是字符串，用来设置线型、颜色、数据点标记。 x、y、z 是向量时，plot3 命令的使用

1
2
3
4
5
6
7
8
9
t=0:0.1:8*pi; 
plot3(sin(t),cos(t),t)
title('绘制螺旋线') 
%用命令 title 对图形主题进行标注 
xlabel('sin(t)')         
ylabel('cos(t)') 
zlabel('t')     
%命令 zlabel 用来指定 z 轴的数据名称 
grid on

x、y、z 都是矩阵时，plot3 命令的使用

1
2
3
[X,Y]=meshgrid(-pi:0.1:pi);
Z=sin(X)+cos(Y); 
plot3(X,Y,Z)

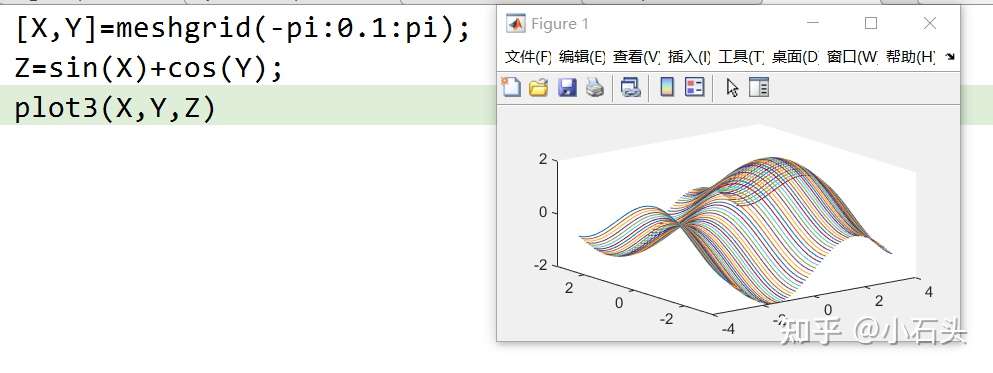
  • 三维曲面绘图命令 ：首先是平面网格点的生成 函数命令meshgrid 用来生成 x-y 平面上的网格点矩阵。 调用形式为：

    1
    2
    [X,Y]=meshgrid(x,y)  
    [X,Y]=meshgrid(x) 等价于[X,Y]=meshgrid(x,x)

参数含义如下： x：是区间[x0,xm]上分划的向量； y：是区间[y0,yn]上分划的向量； X，Y：输出变量矩阵，矩阵 X 的行向量都是向量 x，矩阵 Y 的列向量都是向量 y。 函数 meshgrid 将由两个向量决定的区域转换为对应的网格点矩阵。

  • 三维网格命令 mesh 利用函数mesh生成网格曲面。 调用格式为：
    1. mesh(X，Y，Z，C)：X、Y、Z、C 是同维数的矩阵，X、Y、Z 对应空间上的网格点，网格线颜色由C决定；
    2. mesh(X，Y，Z)：相当于上面的 C=Z 的情况；
    3. mesh(x，y，Z，C)：x 和 y 是向量，Z 和 C 是同维数的矩阵，网格曲面的网格顶点是（ x(j)，y(i)，Z(i,j)），网格线的颜色由矩阵 C 决定；
  • 三维表面命令 surf 函数：surf 命令的调用格式与 mesh 相同。 利用三维网格表面命令 surf 绘制图形。
1
2
3
z=peaks;      %绘制山峰的图像，将函数值赋予变量z 
surf(z)          %对山峰的图像进行着色处理
shading interp  %函数 shading 改变着色方式
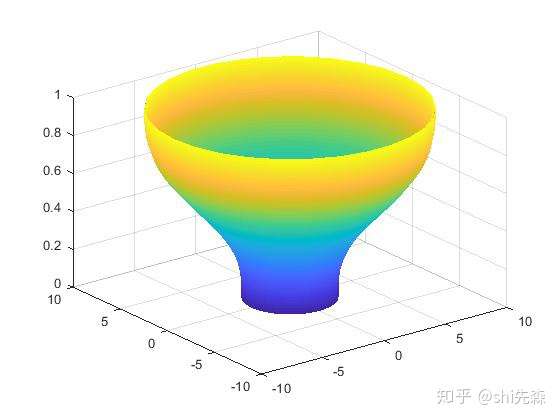
  • 柱面的表达cylinder cylinder命令中，柱面的轴线定义为 z 轴，只要给出母线的描述就可完成一个柱面。 调用格式为：
1
2
3
[X,Y,Z] = cylinder(R,N)；
[X,Y,Z] = cylinder(R)：缺省值 N=20； 
[X,Y,Z] = cylinder：缺省值 N=20，R=[1，1]。

R：是一描述柱面母线的向量； N：是旋转柱面上的分割线条数； [X,Y,Z] ：是返回的x,y,z坐标向量。 绘制一个柱面。

1
2
3
4
t=pi:0.01:3*pi; 
r=sin(t)+t; 
cylinder(r,30) 
shading interp

  • 球面的表达sphere 调用格式为：
    [X,Y,Z]=sphere(N)：产生一个（ N+1）×（ N+1）的矩阵，然后用函数 surf 命令绘制一个单位的球面，N 为设置分割线的条数；
    [X,Y,Z] = sphere：缺省 N = 20。

画一个球面。

1
2
[X,Y,Z]=sphere;
surf(X,Y,Z)

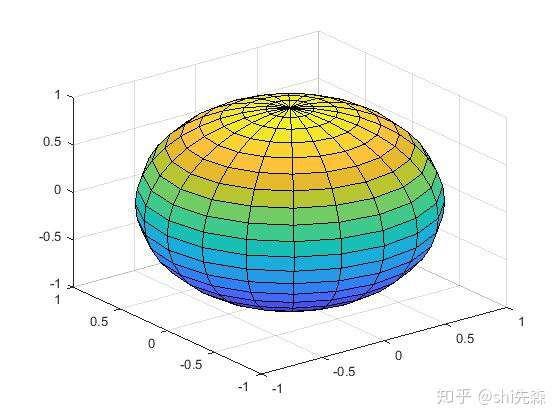
图像标注修饰

  • 图形标注：坐标轴和图形标题标注; 标注坐标轴 x、y 和 z 的命令函数为 xlabel、ylabel 和 zlabel 调用格式为：
1
2
xlabel('text') 
xlabel('text','Property1',PropertyValue1,'Property2',PropertyValue2,...)

图例的标注 legend命令实现不同图例的说明。其调用格式为：

1
2
legend(string1,string2,string3, ...)   
legend(string1,string2,string3,...,Pos)

按顺序把字符串添加到相应的曲线线型符号之后；Pos对图例的位置作出设置和调整：

0 = 自动把图例置于最佳位置（ 和图中曲线重复最少）； 1 = 置于图形窗口的右上角（ 缺省值）； 2 = 置于图形窗口的左上角； 3 = 置于图形窗口的左下角； 4 = 置于图形窗口的右下角； -1 = 置于图形窗口的右侧（ 外部）。

  • 控制分格线 对二维和三维图形都适用。 有三种用法：grid on：打开分格线控制开关，以后绘制的图形都带有分格线； grid off：关闭分格线控制开关，以后绘制的图形都不带分格线； grid：用于实现分格线绘制切换。绘制图形，并用函数 xlabel、title 和 legend 命令进行标注。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
t=0:0.1:4*pi; 
y=sin(t); 
y1=cos(t); 
plot(t,y,':',t,y1,'r*') 
xlabel('x 轴  (0--4\pi)','fontsize',12,'fontweight','bold') 
ylabel('y 轴','fontsize',12,'fontweight','bold') 
title('绘制正弦波和余弦波      Pos=1','fontsize',10,'fontweight','bold','fontangle','italic') 
text(pi,0,'\leftarrowsin(\pi)=0') 
text(pi,-1,'\leftarrowcos(\pi)=-1')
text(pi/2,0.9,['\uparrowsin(\pi/2)=',num2str(sin(pi/2))]) 
legend('正弦波','余弦波') 
figure(2) 
plot(t,y,':',t,y1,'r*') 
title('绘制正弦波和余弦波    Pos=0','fontsize',10,'fontweight','bold','fontangle','italic') 
legend('正弦波','余弦波',0) 
grid on 
figure(3) 
plot(t,y,':',t,y1,'r*') 
title('绘制正弦波和余弦波  Pos=-1','fontsize',10,'fontweight','bold','fontangle','italic')

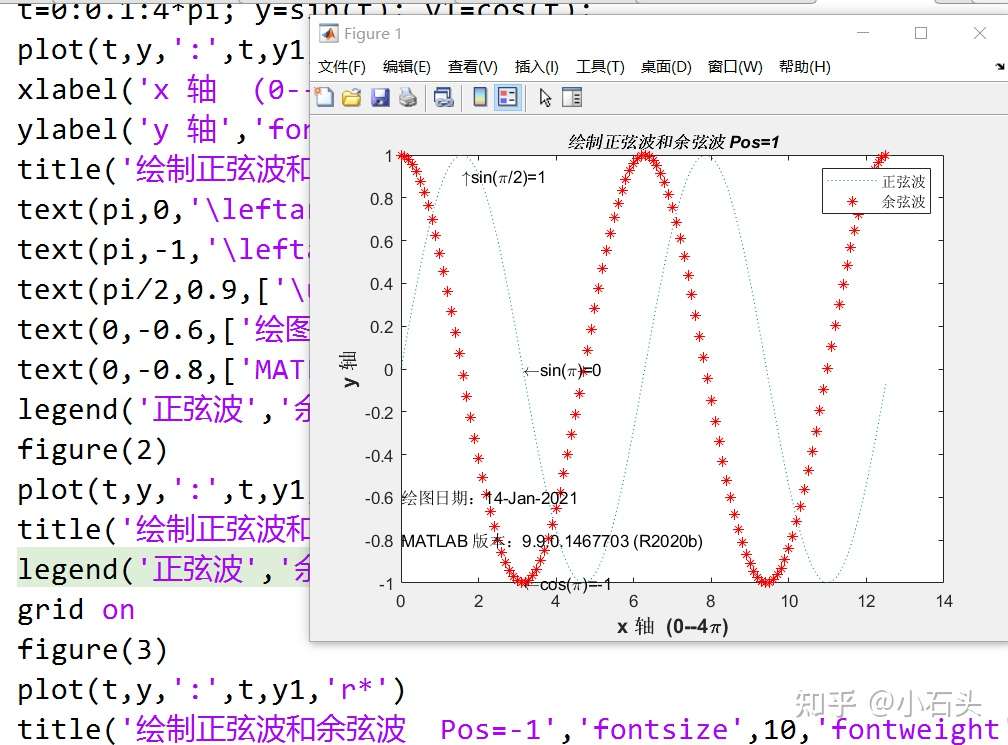
matlab符号运算

符号对象的建立：sym 和 syms

1
符号变量 = sym(A)

syms 符号变量1 符号变量2 … 符号变量n

1
syms a b c

查找符号表达式中的符号变量：findsym(expr) %按字母顺序列出符号表达式 expr 中的所有符号变量；findsym(expr, N)%按顺序列出 expr 中离 x 最近的 N 个符号变量；用给定的数据替换符号表达式中的指定的符号变量

1
subs(f,x,a)

用 a 替换字符函数 f 中的字符变量 x

  • 因式分解
1
2
3
syms x;
f=x^6+1;
factor(f)
  • 函数展开
1
2
3
syms x; 
f=(x+1)^6;
expand(f)
  • 合并同类项
1
collect(f,v) %按指定变量 v 进行合并
  • 函数简化
1
[How,y]=simple(f):   y 为 f  的最简短形式，How 中记录的为简化过程中使用的方法。
  • 计算极限
1
2
3
4
5
limit(f,x,a): 计算
limit(f,a): 当默认变量趋向于 a 时的极限
limit(f): 计算 a=0 时的极限
limit(f,x,a,'right'): 计算右极限
limit(f,x,a,'left'): 计算左极限
  • 计算导数
1
2
3
g=diff(f,v)：求符号表达式  f 关于 v 的导数
g=diff(f)：求符号表达式  f 关于默认变量的导数
g=diff(f,v,n)：求  f 关于 v 的 n 阶导数
  • 计算积分
1
2
3
4
int(f,v,a,b): 计算定积分
int(f,a,b): 计算关于默认变量的定积分
int(f,v): 计算不定积分
int(f): 计算关于默认变量的不定积分
  • 符号求和
1
symsum(f,v,a,b)
  • 代数方程求解 solve(f,v)：求方程关于指定自变量的解
  • 微分方程求解
1
y=dsolve('eq1','eq2', ... ,'cond1','cond2', ... ,'v')

其中 y 为输出的解， eq1、eq2、. . . 为微分方程，cond1、cond2、…为初值条件， v 为自变量

matlab 程序设计

M文件

用MATLAB语言编写的程序，称为M文件。 M文件有两类：

命令文件和函数文件。 命令文件：没有输入参数，也不返回输出参数。

函数文件：可以输入参数，也可返回输出参数。

  • input函数： 用于向计算机输入一个参数;
  • pause函数：暂停程序的执行;
  • disp函数：命令窗口输出函数。

程序设计

- for语句：格式：

1
2
3
for 循环变量=表达式1:表达式2:表达式3
    循环体语句
end

注：其中表达式1的值为循环变量的初值，表达式2的值为步长，表达式3的值为循环变量的终值。步长为1时，表达式2可以省略

  • while语句: 格式为：
1
2
3
while (条件)
    循环体语句
end

函数

函数是一起执行任务的一组语句。在MATLAB中，函数是在单独的文件中定义的。文件名和函数名应该相同。

函数在其自己的工作空间（也称为本地工作空间）中对变量进行操作，与在MATLAB命令提示符下访问的工作空间（称为基本工作空间）不同。

函数可以接受多个输入参数，并且可以返回多个输出参数。

函数语句的语法是-

1
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)

注：其中函数名的命名规则与变量名相同。输入形参为函数的输入参数，输出形参为函数的输出参数。当输出形参多于1个时，则应该用方括号括起来。

编写函数文件求小于任意自然数n的Fibonacci数列各项。

1
2
3
4
5
6
7
8
function f=ffib(n)
   %用于求Fibonacci数列的函数文件
   f=[1,1];
   i=1;
   while f(i)+f(i+1)<n
      f(i+2)=f(i)+f(i+1);
      i=i+1;
   end
  • 函数调用： [输出实参表]=函数名(输入实参表)

匿名函数

匿名函数就像传统编程语言中的内联函数一样，是在单个MATLAB语句中定义的。它由一个MATLAB表达式以及任意数量的输入和输出参数组成。

您可以直接在MATLAB命令行或在函数或脚本中定义匿名函数。

这样，您可以创建简单的功能，而不必为其创建文件。

从表达式创建匿名函数的语法是

1
f = @(arglist)expression

实例

在此示例中，我们将编写一个名为power的匿名函数，该函数将两个数字作为输入，并将第一个数字提高为第二个数字的幂。

创建一个脚本文件并在其中键入以下代码-

示例

1
2
3
4
5
power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

运行文件时，它显示-

1
2
3
4
result1 =  343
result2 =  7
result3 =  1.0000e-10
result4 =  9.5459

主和子函数

必须在文件中定义除匿名函数以外的任何函数。每个函数文件都包含一个首先出现的必需主函数，以及在主函数之后并由其使用的任意数量的可选子函数。

可以从定义主文件的文件外部（从命令行或其他函数）调用主函数，但是不能从命令行或其他函数在功能文件外部调用子函数。

子函数仅对主函数和定义它们的函数文件中的其他子函数可见。

实例

让我们写一个名为quadratic的函数来计算一个二次方程的根。该函数包含三个输入：二次系数、线性系数和常数项。它将回归根。

函数文件quadratic.m将包含主函数quadratic和子函数disc，后者计算判别式。

创建一个函数文件 quadratic.m 并在其中输入以下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function [x1,x2] = quadratic(a,b,c)

%此函数返回
%二次方程。
%它需要3个输入参数
%x2，x和
%常数项
%它返回根
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of quadratic

function dis = disc(a,b,c) 
%函数计算判别式
dis = sqrt(b^2 - 4*a*c);
end   % end of sub-function

您可以从命令提示符处调用上述功能，如下所示：

1
quadratic(2,4,-4)

MATLAB将执行上述语句并返回以下结果-

1
ans = 0.7321

嵌套函数

您可以在另一个函数的主体内定义函数。这些称为嵌套函数。嵌套函数包含任何其他函数的任何或所有组件。

嵌套函数在另一个函数的范围内定义，它们共享对包含函数的工作区的访问。

嵌套函数遵循以下语法-

1
2
3
4
5
6
7
8
function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

实例

让我们重写前面实例中的quadratic函数，不过，这次disc函数将是一个嵌套函数。

创建一个函数文件quadratic2.m，并在其中输入以下代码-

1
2
3
4
5
6
7
8
9
function [x1,x2] = quadratic2(a,b,c)
function disc  %嵌套函数
d = sqrt(b^2 - 4*a*c);
end   % 结束函数disc

disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   %结束函数 quadratic2

您可以从命令提示符处调用上述函数，如下所示：

1
quadratic2(2,4,-4)

MATLAB将执行上述语句并返回以下结果-

1
ans =  0.73205

私有函数

私有函数是仅对有限的一组其他函数可见的主函数。如果不想公开函数function(s)的实现，可以将它们创建为私有函数。

私有函数位于具有特殊名称 Private 的子文件夹中。

它们仅对父文件夹中的函数可见。

实例

让我们重写quadratic函数。不过，这一次，disc函数计算判别式，将是一个私有函数。

在工作目录文件夹中创建一个名为 private 的子文件夹，在其中存储以下函数文件 disc.m

1
2
3
4
function dis = disc(a,b,c) 
%函数计算判别式
dis = sqrt(b^2 - 4*a*c);
end      %子函数结束

在您的工作目录中创建一个函数 quadratic3.m ，并在其中输入以下代码-

1
2
3
4
5
6
7
8
9
10
11
12
13
function [x1,x2] = quadratic3(a,b,c)

% 这个函数返回
% 一元二次方程。
它需要3个输入参数
% 它们是 x2，x 和
% 常数项
% 它返回根
d = disc(a,b,c); 

x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end      %结束 quadratic3

您可以从命令提示符处调用上述函数，如下所示：

1
quadratic3(2,4,-4)

MATLAB将执行上述语句并返回以下结果-

1
ans =  0.73205

全局变量

全局变量可以由多个函数共享。为此，您需要在所有函数中将变量声明为全局变量。

如果要从基本工作空间访问该变量，请在命令行中声明该变量。

全局声明必须在变量实际在函数中使用之前发生。最好将大写字母用作全局变量的名称，以将其与其他变量区分开。

实例

让我们创建一个名为average.m的函数文件，并在其中输入以下代码-

1
2
3
4
function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end

创建一个脚本文件并在其中键入以下代码-

1
2
3
4
global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)

运行文件时，它将显示以下结果-

1
av =  35.500

matlab数据

MATLAB 数据导入（ImportData）

在MATLAB中导入数据意味着从外部文件加载数据。该importdata功能允许加载不同格式的各种数据文件。它具有以下五种形式-

序号 功能说明
1 *A = importdata(filename)*从filename*表示的文件*中将数据加载到数组A中。
2 **A = importdata(‘-pastespecial’)**从系统剪贴板而不是文件加载数据。
3 **A = importdata(___, delimiterIn)**将 delimiterIn 解释为 ASCII 文件、文件名或剪贴板数据中的列分隔符。可以对上述语法中的任何输入参数使用 delimiterIn。
4 **A = importdata(___, delimiterIn, headerlinesIn)*从ASCII文件，文件名或剪贴板中加载数据，并从行headerlinesIn + 1*开始读取数字数据。
5 **[A, delimiterOut, headerlinesOut] = importdata(___)**使用前面语法中的任何输入参数，返回delimiterOut中输入ASCII文件的检测到的分隔符字符和headerlinesOut中检测到的头行数。

默认情况下，Octave不支持该*importdata()*功能，因此您必须搜索并安装此软件包才能使以下示例适用于Octave安装。

实例1

让我们加载并显示图像文件。创建一个脚本文件并在其中键入以下代码-

1
2
3
filename = 'smile.jpg';
A = importdata(filename);
image(A);

运行文件时，MATLAB将显示图像文件。但是，必须将其存储在当前目录中。

实例2

在此示例中，我们导入一个文本文件并指定Delimiter和Column Header。让我们创建一个以空格分隔的ASCII文件，其中包含标题为weeklydata.txt的列标题。

我们的文本文件weeklydata.txt看起来像这样-

1
2
3
4
5
6
SunDay  MonDay  TuesDay  WednesDay  ThursDay  FriDay  SaturDay
95.01   76.21   61.54    40.57       55.79    70.28   81.53
73.11   45.65   79.19    93.55       75.29    69.87   74.68
60.68   41.85   92.18    91.69       81.32    90.38   74.51
48.60   82.14   73.82    41.03       0.99     67.22   93.18
89.13   44.47   57.63    89.36       13.89    19.88   46.60

创建一个脚本文件并在其中键入以下代码-

1
2
3
4
5
6
7
8
9
10
11
filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);

% View data
for k = [1:7]
   disp(A.colheaders{1, k})
   disp(A.data(:, k))
   disp(' ')
end

运行文件时，它显示以下结果-

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
SunDay
   95.0100
   73.1100
   60.6800
   48.6000
   89.1300
 
MonDay
   76.2100
   45.6500
   41.8500
   82.1400
   44.4700
 
TuesDay
   61.5400
   79.1900
   92.1800
   73.8200
   57.6300

WednesDay
   40.5700
   93.5500
   91.6900
   41.0300
   89.3600
 
ThursDay
   55.7900
   75.2900
   81.3200
   0.9900
   13.8900
 
FriDay
   70.2800
   69.8700
   90.3800
   67.2200
   19.8800

SaturDay
   81.5300
   74.6800
   74.5100
   93.1800
   46.6000

实例3

在此示例中，让我们从剪贴板导入数据。

将以下行复制到剪贴板-

Mathematics is simple

创建一个脚本文件并输入以下代码-

1
A = importdata('-pastespecial')

运行文件时，它显示以下结果-

1
2
A = 
   'Mathematics is simple'

底层文件I / O

importdata函数是一个高级函数。MATLAB中的底层文件I/O函数允许对文件的读写数据进行最大程度的控制。但是，这些函数需要更详细的文件信息才能有效地工作。

MATLAB为字节或字符级别的读写操作提供以下函数-

函数 描述
fclose 关闭一个或所有打开的文件
feof 文件结尾测试
ferror 有关文件I/O错误的信息
fgetl 从文件中读取行，删除换行符
fgets 从文件中读取行，保留换行符
fopen 打开文件，或获取有关打开文件的信息
fprintf 将数据写入文本文件
fread 从二进制文件读取数据
frewind 将文件位置指示器移动到打开文件的开头
fscanf 从文本文件读取数据
fseek 移动到文件中的指定位置
ftell 在打开文件中的位置
fwrite 将数据写入二进制文件

导入具有底层I / O的文本数据文件

MATLAB提供以下功能用于文本数据文件的底层导入-

  • fscanf函数读取文本或ASCII文件中的格式化数据。
  • fgetl和fgets的时间，其中，一个换行字符的每一行分离功能读取的文件的一行。
  • fread函数读取字节或位级别的数据流。

MATLAB 数据输出

数据导出(或输出)在 MATLAB 的意思是写入文件。MATLAB 允许您在另一个读取 ASCII 文件的应用程序中使用您的数据。为此，MATLAB 提供了几个数据导出选项。

您可以创建以下类型的文件-

  • 数组中的矩形、分隔的ASCII数据文件。
  • 击键的日记（或日志）文件和结果文本输出。
  • 使用底层函数（如fprintf）的专用ASCII文件。
  • MEX文件，用于访问以特定文本文件格式写入的C / C ++或Fortran例程。

除此之外，您还可以将数据导出到电子表格。

有两种方法可以将数字数组导出为定界的ASCII数据文件-

  • 使用save函数并指定**-ascii**限定符
  • 使用dlmwrite函数

使用save函数的语法是-

1
save my_data.out num_array -ascii

其中，my_data.out是创建的带分隔符的ASCII数据文件，num_array是数字数组，并且 −ascii是说明符。

使用dlmwrite函数的语法是-

1
dlmwrite('my_data.out', num_array, 'dlm_char')

其中，my_data.out是创建的带分隔符的ASCII数据文件，num_array是数字数组， dlm_char是分隔符。

在线示例

下面的示例演示了该概念。创建一个脚本文件并输入以下代码-

示例

1
2
3
4
5
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out

运行文件时，它显示以下结果-

1
2
3
4
5
6
7
   1.0000000e+00   2.0000000e+00   3.0000000e+00   4.0000000e+00
   4.0000000e+00   5.0000000e+00   6.0000000e+00   7.0000000e+00
   7.0000000e+00   8.0000000e+00   9.0000000e+00   0.0000000e+00

1 2 3 4
4 5 6 7
7 8 9 0

请注意，save -ascii命令和dlmwrite函数不适用于作为输入的单元格数组。要从单元格数组的内容创建定界的ASCII文件，您可以

  • 使用cell2mat函数将单元格数组转换为矩阵
  • 或使用底层文件I / O功能导出单元数组。

如果使用save函数将字符数组写入ASCII文件，则它将等效于字符的ASCII写入文件。

例如，让我们将单词“ hello”写到文件中-

示例

1
2
3
h = 'hello';
savetextdata.outh -ascii
type textdata.out

MATLAB执行以上语句并显示以下结果。这是8位ASCII格式的字符串“ hello”的字符。

1
1.0400000e+02   1.0100000e+02   1.0800000e+02   1.0800000e+02   1.1100000e+02

写入日记文件

日记文件是您的MATLAB会话的活动日志。日记功能可以在磁盘文件中创建会话的精确副本，但不包括图形。

要打开日记函数，请输入-

1
diary

（可选）您可以提供日志文件的名称，例如-

1
diary logdata.out

关闭日记函数-

1
diary off

您可以在文本编辑器中打开日记文件。

使用底层I / O将数据导出到文本数据文件

到目前为止，我们已经导出了数字数组。但是，您可能需要创建其他文本文件，包括数字和字符数据的组合，非矩形输出文件或具有非ASCII编码方案的文件。为此，MATLAB提供了底层fprintf函数。

与在底层I / O文件活动中一样，在导出之前，您需要使用fopen函数打开或创建文件并获取文件标识符。默认情况下，fopen打开文件以进行只读访问。您应指定写入或追加的权限，例如“ w”或“ a”。

处理完文件后，需要使用**fclose(fid)**函数将其关闭。

以下示例演示了概念-

实例

创建一个脚本文件并在其中键入以下代码-

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
%创建一个包含两行的矩阵y
x = 0:10:100;
y = [x; log(x)];
 
%打开文件进行写入
fid = fopen('logtable.txt', 'w');
 
%表格标题
fprintf(fid, 'Log     Function\n\n');
 
%按列顺序打印值
%文件的每一行上显示两个值
fprintf(fid, '%f    %f\n', y);
fclose(fid);

%显示创建的文件
type logtable.txt

运行文件时，它显示以下结果-

1
2
3
4
5
6
7
8
9
10
11
12
13
Log         Function

0.000000    -Inf
10.000000    2.302585
20.000000    2.995732
30.000000    3.401197
40.000000    3.688879
50.000000    3.912023
60.000000    4.094345
70.000000    4.248495
80.000000    4.382027
90.000000    4.499810
100.000000    4.605170
数学 > 数模
#Matlab入门
Matlab入门
http://mavericreate.top/Blogs/2025/08/28/Matlab入门/
作者
唐浩天
发布于
2025年8月28日
许可协议